4. Functions¶

4.1. Functions¶

In Python, a function is a named sequence of statements that belong together. Their primary purpose is to help us organize programs into chunks that match how we think about the problem.

The syntax for a function definition is:

def NAME( PARAMETERS ):
    STATEMENTS

You can make up any names you want for the functions you create, except that you can’t use a name that is a Python keyword, and the names must follow the rules for legal identifiers. The parameters specifies what information, if any, you have to provide in order to use the new function.

There can be any number of statements inside the function, but they have to be indented from the def. In the examples in this book, we will use the standard indentation of four spaces. Function definitions are the second of several compound statements we will see, all of which have the same pattern:

A header which begins with a keyword and ends with a colon (:).
A body consisting of one or more Python statements, each indented the same amount – 4 spaces is the Python standard – from the header line.

We’ve already seen the for loop which follows this pattern.

In a function definition, the keyword in the header is def, which is followed by the name of the function and some parameters enclosed in parentheses. The parameter list may be empty, or it may contain any number of parameters separated from one another by commas. In either case, the parentheses are required.

Suppose we’re working with turtles, and a common operation we need is to draw squares. “Draw a square” is an abstraction, or a mental chunk, of a number of smaller steps. So let’s write a function to capture the pattern of this “building block”:

import turtle


def draw_square(t, size):
    """Make turtle t draw a square with sides of length, size."""

    for i in range(4):
        t.forward(size)
        t.left(90)

turtle.setup(800, 600)
wn = turtle.Screen()
wn.bgcolor("lightgreen")
wn.title("Alex meets a function")

alex = turtle.Turtle()

# call with draw_square function with turtle, alex, and size, 250
draw_square(alex, 250)

wn.exitonclick()

As usual, run this program and look at what it does.

The function in this program is named draw_square. It has two parameters – one to tell the function which turtle to move around, and the other to tell it the size of the square we want drawn. Make sure you know where the body of the function ends – it depends on the indentation, and the blank lines don’t count for this purpose!

docstrings

If the first thing in a function body is a string, it is called a docstring and gets special treatment in Python.
If the first line in a Python script (module) is a string, it is also a docstring. You saw this in the previous chapter in the exercises that used doctest.
Another way to retrieve this information is to use the interactive interpreter, and enter the expression <function_name>.__doc__, which will retrieve the docstring for the function. So the string you write as documentation at the start of a function is retrievable by python tools at runtime. This is different from comments in your code, which are completely eliminated when the program is parsed.
By convention, Python programmers use docstrings for the key documentation of their functions.

Defining a new function does not make the function run. To do that we need a function call. We’ve already seen how to call some built-in functions like print, range and int. Function calls contain the name of the function being executed followed by a list of values, called arguments, which are assigned to the parameters in the function definition. So in the second last line of the program, we call the function, and pass alex as the turtle to be manipulated, and 50 as the size of the square we want.

Once we’ve defined a function, we can call it as often as we like, and its statements will be executed each time we call it. And we could use it to get any of our turtles to draw a square. In the next example, we’ve changed the draw_square function a little, and we get tess to draw 15 squares, with some variations.

import turtle


def draw_multicolor_square(t, sz):
    """Make turtle t draw a multi-color square of sz."""
    for c in ['red', 'purple', 'hotpink', 'blue']:
        t.color(c)
        t.forward(sz)
        t.left(90)

# Set up the window and its attributes
turtle.setup(800, 600)
wn = turtle.Screen()
wn.bgcolor("lightgreen")
wn.title("Spiralling Squares")

# create tess and set some attributes
tess = turtle.Turtle()
tess.pensize(3)

size = 20                        # size of the smallest square
for i in range(25):
    draw_multicolor_square(tess, size)
    size = size + 10             # increase the size for next time
    tess.forward(10)             # move tess along a little
    tess.right(18)               # and give her some extra turn

wn.exitonclick()

When you run this program, it will generate

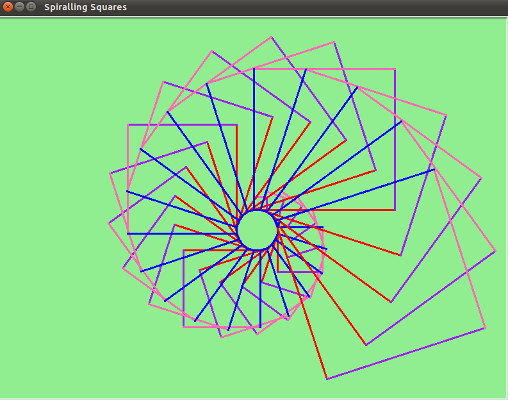
4.2. Functions can call other functions¶

What if we want a function to draw a rectangle? We will need separate arguments for width and height, and a change in the loop logic to the handle the fact that all four sides are not equal.

def draw_rectangle(t, w, h):
    """Get turtle t to draw a rectangle of width w and height h."""
    for i in range(2):
        t.forward(w)
        t.left(90)
        t.forward(h)
        t.left(90)

The parameter names are deliberately chosen as single letters to ensure they’re not misunderstood. In real programs, once you’ve had more experience, we will insist on better variable names than this.

But the point is that the program doesn’t “understand” that you’re drawing a rectangle, or that the parameters represent the width and the height. Concepts like rectangle, width, and height are the meaning we humans have, not concepts that the program or the computer understands.

Thinking like a scientist involves looking for patterns and relationships. In the code above, we’ve done that to some extent. We did not just draw four sides. Instead, we spotted that we could draw the rectangle as two halves, and used a loop to repeat that pattern twice.

But now we might spot that a square is a special kind of rectangle. We already have a function that draws a rectangle, so we can use that to draw our square.

def draw_square(tx, sz):        # a new version of draw_square
    draw_rectangle(tx, sz, sz)

There are some points worth noting here:

Functions can call other functions.
Rewriting draw_square like this captures the relationship between rectangles and squares.
A caller of this function might say draw_square(tess, 50). The parameters of this function, tx and sz, are assigned the values of the tess object, and the int 50 respectively.
In the body of the function they are just like any other variable.
When the call is made to draw_rectangle, the values in variables tx and sz are fetched first, then the call happens. So as we enter the top of function draw_rectangle, its variable t is assigned the tess object, and w and h in that function are both given the value 50.

So far, it may not be clear why it is worth the trouble to create all of these new functions. Actually, there are a lot of reasons, but this example demonstrates two:

Creating a new function gives you an opportunity to name a group of statements. Functions can simplify a program by hiding a complex computation behind a single command. The function (including its name) can capture your mental chunking, or abstraction, of the problem.
Creating a new function can make a program smaller by eliminating repetitive code.

As you might expect, you have to create a function before you can execute it. In other words, the function definition has to be executed before the first time it is called.

4.3. Flow of execution¶

In order to ensure that a function is defined before its first use, you have to know the order in which statements are executed, which is called the flow of execution. We’ve already talked about this a little in the previous chapter.

Execution always begins at the first statement of the program. Statements are executed one at a time, in order from top to bottom.

Function definitions do not alter the flow of execution of the program, but remember that statements inside the function are not executed until the function is called. Although it is not common, you can define one function inside another. In this case, the inner definition isn’t executed until the outer function is called.

Function calls are like a detour in the flow of execution. Instead of going to the next statement, the flow jumps to the first line of the called function, executes all the statements there, and then comes back to pick up where it left off.

That sounds simple enough, until you remember that one function can call another. While in the middle of one function, the program might have to execute the statements in another function. But while executing that new function, the program might have to execute yet another function!

Fortunately, Python is adept at keeping track of where it is, so each time a function completes, the program picks up where it left off in the function that called it. When it gets to the end of the program, it terminates.

What’s the moral of this sordid tale? When you read a program, don’t read from top to bottom. Instead, follow the flow of execution.

4.4. Functions that return values¶

Most functions require arguments, values that control how the function does its job. For example, if you want to find the absolute value of a number, you have to indicate what the number is. Python has a built-in function for computing the absolute value:

>>> abs(5)
5
>>> abs(-5)
5

In this example, the arguments to the abs function are 5 and -5.

Some functions take more than one argument. For example the built-in function pow takes two arguments, the base and the exponent. Inside the function, the values that are passed get assigned to variables called parameters.

>>> pow(2, 3)
8
>>> pow(7, 4)
2401

Another built-in function that takes more than one argument is max.

>>> max(7, 11)
11
>>> max(4, 1, 17, 2, 12)
17
>>> max(3 * 11, 5**3, 512 - 9, 1024**0)
503

max can be sent any number of arguments, separated by commas, and will return the maximum value sent. The arguments can be either simple values or expressions. In the last example, 503 is returned, since it is larger than 33, 125, and 1.

Furthermore, functions like range, int, abs all return values that can be used to build more complex expressions.

So an important difference between these functions and one like draw_square is that draw_square was not executed because we wanted it to compute a value — on the contrary, we wrote draw_square because we wanted it to execute a sequence of steps that caused the turtle to draw.

Functions that return values are called fruitful functions in this course. In some programming languages, a function that does not return a value is called a procedure, since it is used to implement procedural abstraction, but in Python both constructs are just called functions.

How do we write our own fruitful functions? We will start by looking at a few functions from Algebra and seeing how they are written in Python.

Here is a linear function as it would appear in Algebra:

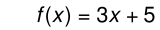
Here is the same function written in Python:

def f(x):
    return 3 * x + 5

Another example of a quadratic function in Algebra:

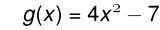
The same function written in Python:

def g(x):
    return 4 * x ** 2 - 7

The return statement is followed an expression which is evaluated. Its result is returned to the caller as the “fruit” of calling this function.

To test these functions and see how the values they return can be used by the calling program, let’s first put them in our own Python module. We were introduced to modules in the last chapter when we used the turtle module. Now we will make our own.

Create a file named algebra_functions.py containing the function definitions for f and g.

Start a Python shell from the same directory in which algebra_functions.py is located, and try these commands at the Python prompt

>>> from algebra_functions import f, g
>>> f(0)
5
>>> g(0)
-7
>>> g(2)
9
>>> f(9)
32
>>> returned_value = g(2)
>>> returned_value
9
>>> f(returned_value)
32
>>> f(g(2))
32
>>>

Some things to learn from this example:

The import statement can be used to read our own Python code into the Python shell.

We can thus write our functions in a module and then import them into the Python shell so that we can experiment with them.
The import statement has two forms
```
import MODULE

from MODULE import FUNCTION, FUNCTION, ...
```
We used the first form last chapter when importing the turtle module. If we used that same form this time, our Python shell session would have started like this
```
>>> import algebra_functions
>>> algebra_functions.f(0)
5
>>> algebra_functions.g(0)
-7
```
We will be discussing the use of the import statement further later on. For now just be able to use this new form to read your own functions into a Python shell so you can experiment with them.
Lines 2, 4, 6, and 8 are simple function calls to the two functions imported from our module. In the Python shell, returned values are displayed on the lines following each function call. We can say that the function call evaluates to the returned value.
In line 10 the value returned from calling g with 2 as an argument is assigned to a variable named returned_value. When a variable name is entered at the Python shell, the interpreter prints out its value.
In line 13, the returned_value variable is sent as an argument to f. Since we know returned_value holds 9, it should come as no surprise that the lines following 8 and 13 are the same.
Line 15 is an example of function composition, in which the output of one function call is sent as input to another. In this case, a call to f is composed with a call to g. Since g(2) returns 9, f(g(2)) returns 32.

4.5. Naming variables¶

For one more example of a fruitful function, let’s revisit the compound interest exercise we saw in chapter 2, this time writing it as a function.

Here again is a description of the function:

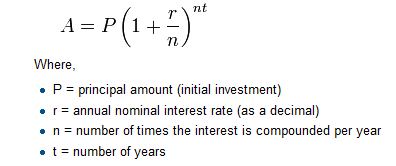
And here is a Python program that implements that function:

def final_amt(p, r, n, t):
    """
      Apply the compound interest formula to p
      to produce the final amount.
    """
    return p * (1 + r / n) ** (n * t)


# now that we have the function above, let us call it.
to_invest = float(input("How much do you want to invest? "))
fnl = final_amt(to_invest, 0.08, 12, 5)
print("At the end of the period you'll have $", fnl)

We prompted the user for the principal amount. The type of to_invest is a string, but we need a number before we can work with it. Because it is money, and could have decimal places, we’ve used the float type converter function to parse the string and return a float.
Notice how we entered the arguments for 8% interest, compounded 12 times per year, for 5 years.
When we run this program and enter 100 at the How much do you want to invest? prompt, we get the output:
```
At the end of the period you'll have $ 148.9845708301605
```
This is a bit messy with all these decimal places, but remember that Python doesn’t understand that you’re working with money: it just does the calculation to the best of its ability, without rounding. Later we’ll show you how to format the string that is printed in such a way that it does get nicely rounded to two decimal places before printing.
The line to_invest = float(input("How much do you want to invest?")) also shows another example of composition – we can call a function like float, and its arguments can be the results of other function calls (like input) that we’ve called along the way.

Notice something else very important here. The name of the variable we pass as an argument – to_invest – has nothing to do with the name of the parameter – p. It is as if p = to_invest is executed when final_amt is called. It doesn’t matter what the value was named in the caller, in final_amt it’s name is p.

def final_amt(p, r, n, t):
    return p * (1 + r / n) ** (n * t)

This equation is getting rather complex, and it is becoming increasingly challenging to keep track of what each variable is being used for. Whenever you find yourself having difficulty remembering which variable is holding which value in your program, it is advisable to choose variable names that better describe what they represent.

Here are three other ways we could have written our function, with variable names of different lengths:

def final_amt_v2(principal_amount, nominal_percentage_rate,
                 num_times_per_year, years):
    return principal_amount * \
           (1 + nominal_percentage_rate / num_times_per_year) ** \
           (num_times_per_year * years)


def final_amt_v3(principal_amount, nominal_percentage_rate,
                 num_times_per_year, years):
    return (principal_amount *
           (1 + nominal_percentage_rate / num_times_per_year) **
           (num_times_per_year * years))


def final_amt_v4(amt, rate, compounded, years):
    return amt * (1 + rate / compounded) ** (compounded * years)

A few new bits of Python to learn from this example:

Long logical lines can be broken into shorter physical lines using explicit line joining with the backslash (\) character.
Long expressions enclosed in paranthesis (()), square brackets ([]), and curly braces ({}) can be broken across multiple lines using implicit line joining.

Each of these variations do the same thing, but they vary in terms of readability. Which one is best?

It is a good rule of thumb to use descriptive variable names to make your code self documenting, but there is more art to this than science.

The names choosen in versions 2 and 3 are so long they require the use of either explicit or implicit line joining to keep lines within the Python Style guide‘s recommended 79 character line length.

The names in this version are probably too long. Readability is hurt by the need to follow the expression over multiple lines.

Version 4 may be the sweet spot – descriptive enough names to be self documenting, but short enough to make the entire expression readable.

PEP8 - The Python Style Guide

Readability is very important to programmers, since in practice programs are read and modified far more often then they are written. All the code examples in this book will be consistent with the Python Enhancement Proposal 8 (PEP 8), a style guide developed by the Python community.

We’ll have more to say about style as our programs become more complex, but a few pointers will be helpful already:

use 4 spaces for indentation
imports should go at the top of the file
separate function definitions with two blank lines
keep function definitions together
keep top level statements, including function calls, together at the bottom of the program

4.6. Turtles Revisited¶

Now that we have functions, we can focus our attention on reorganizing our code so that it fits more nicely into our mental chunks. This process of rearrangement is called refactoring the code. The resulting procedural abstraction will make it much easier to write larger, more complex programs.

Two things we’re always going to want to do when working with turtles is to create the window for the turtle, and to create one or more turtles. In four_turtles.py we create functions to do each of those tasks. We also create a function to make a turtle draw a square of a desired size at a desired location:

import turtle


def make_window(color, title):
    """
      Set up the window with the given background color and title.
      Returns the new window.
    """
    turtle.setup(800, 600)
    w = turtle.Screen()
    w.bgcolor(color)
    w.title(title)
    return w


def make_turtle(color, size, shape):
    """
      Set up a turtle with the given color and pensize.
      Returns the new turtle.
    """
    t = turtle.Turtle()
    t.color(color)
    t.pensize(size)
    t.shape(shape)
    return t


def draw_square(t, size, x, y):
    """
      Use turtle, t, to draw a square of size, size, starting with a lower
      left hand corner at x, y.  Returns the turtle to its previous state
      after drawing the square.
    """
    # Store the location and direction of the turtle
    tx = t.xcor()
    ty = t.ycor()
    th = t.heading()

    # Move the turtle to lower left corner of square facing East (heading 0)
    t.penup()
    t.setpos(x, y)
    t.setheading(0)
    t.pendown()

    # Draw the square
    for i in range(4):
        t.forward(size)
        t.left(90)

    # Return turtle to original location and direction
    t.penup()
    t.setpos(tx, ty)
    t.setheading(th)


wn = make_window("lightgreen", "Tess, Alex, Dave, and Jaunice")

tess = make_turtle("hotpink", 5, "arrow")
alex = make_turtle("black", 1, "turtle")
dave = make_turtle("yellow", 2, "circle")
jaunice = make_turtle("red", 3, "triangle")

draw_square(tess, 50, -225, 125)
draw_square(alex, 100, 150, 100)
draw_square(dave, 200, -300, -250)
draw_square(jaunice, 150, 125, -225)

wn.exitonclick()

Running this program generatates this

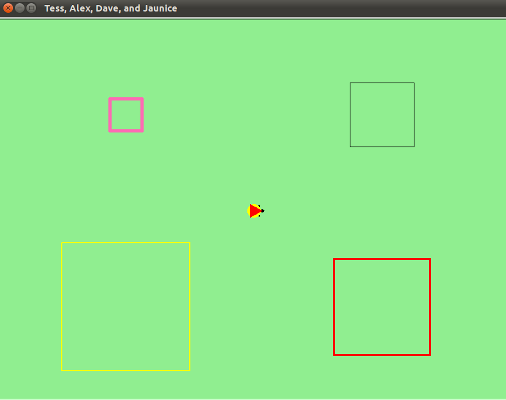
New things to learn about turtles from this example:

Turtles have methods xcor() and ycor() that return their x and y locations, respectively. They also have a method, setpos(), that takes two arguments for x and y and moves the turtle to that location.
Turtles have a method heading() that returns the direction which the turtle is facing. The corresponding setheading() method takes a direction as an argument and points the turtle in that direction.
The default turle shape is arrow, and in addition to the previously seen turtle shape, circle and triangle are valid arguments to the shape() method.

Refactoring refers to any rewrite of program code that does not change the output of the program, but improves the program in terms of readability, efficiency, or maintainability.

The specific refactoring we have been doing is called wrapping code in a function. We have taken sequences of programming statements and moved them from the main module level into the body of a function.

The trick with this kind of refactoring is to see which things you are likely to want to change each time you call the function: these should become the parameters, or changeable bits, of the functions you write.

4.7. Glossary¶

abstraction

The process of generalizing in order to manage intellectual complexity. It may involve identifying common elements between different instances, or identifying the most important elements of a given instance and intentionally disregarding other elements.

Procedural abstraction involves wrapping a set of programming instructions in a function, thus giving the procedure a single name which can then be used in defining more complex procedures.

It is the power of abstraction that makes the creation of large, complex software systems possible.

argument

A value provided to a function when the function is called. This value is assigned to the corresponding parameter in the function. The argument can be the result of an expression which may involve operators, operands and calls to other fruitful functions.

body

The second part of a compound statement. The body consists of a sequence of statements all indented the same amount from the beginning of the header. The standard amount of indentation used within the Python community is 4 spaces.

compound statement

A statement that consists of two parts:

header - which begins with a keyword determining the statement type, and ends with a colon.
body - containing one or more statements indented the same amount from the header.

The syntax of a compound statement looks like this:

keyword expression:
    statement
    statement ...

docstring

A string occurring as the first line of a module or function body (or other things that we will see later). Docstrings are available to Python at run time through an object’s __doc__ attribute.

flow of execution

The order in which statements are executed during a program run.

function

A named sequence of statements that performs some useful operation. Functions may or may not take parameters and may or may not produce a result.

function call

A statement that executes a function. It consists of the name of the function followed by a list of arguments enclosed in parentheses.

function composition

Using the output from one function call as the input to another.

function definition

A statement that creates a new function, specifying its name, parameters, and the statements it executes.

fruitful function

A function that returns a value when it is called.

header line

The first part of a compound statement. A header line begins with a keyword and ends with a colon (:)

import statement

A statement which permits functions and variables defined in another Python module to be brought into the environment of another script.

The import statement can be used in two forms:

import MODULE

from MODULE import FUNCTION1, FUNCTION2, ...

The first form requires the module name to be written followed by a dot (.) in front of the imported function names.

lifetime

Variables and objects have lifetimes — they are created at some point during program execution, and will be destroyed at some time.

local variable

A variable defined inside a function. A local variable can only be used inside its function. Parameters of a function are also a special kind of local variable.

nested loop

A loop which is inside the body of another loop. The number of times a statement inside the body of a nested loop will execute is determined by the product of the number of times the outer loop executes and the number of times the nested loop executes.

parameter

A name used inside a function to refer to the value which was passed to it as an argument.

refactor

A fancy word to describe reorganizing your program code, usually to make it more understandable, more efficient, or more maintainable.

Typically, we have a program that is already working, then we go back to “tidy it up”. It often involves choosing better variable names, or spotting repeated patterns and wrapping that code in a function.

temporary variable

A variable used to store an intermediate value in a complex calculation.

traceback

A list of the functions that are executing, printed when a runtime error occurs. A traceback is also commonly refered to as a stack trace, since it lists the functions in the order in which they are stored in the runtime stack.

wrapping in a function

The process of moving a sequence of programming statements into the body of a function and providing parameters which can be passed to the function.

Wrapping code in a function enables it to be reused, with the data input controlled through arguments passed in with function calls.

4.8. Exercises¶

Create a file named ch04e01.py. Copy the make_window, make_turtle, and draw_square functions you met in TurtlesRevisited above into this file.

Use these functions to write a program that will draw the image shown below in the center of the output window.

Hint

The sides of the squares are 20 units and the squares are 20 units apart. The starting x positions are given by the list [-120, -80, -40, 0, 40, 80, 120] with y starting at 0.
Write a program to draw this.

Hint

Create variables x, y, and length with initial values of 20, 20, and 100, respectively. Inside the body of the loop, make x and y bigger by 10, and length smaller by 20.
Write a non-fruitful function draw_poly(t, n, size, x, y) which makes a turtle draw a regular polygon. When called with draw_poly(tess, 8, 50, 0, 0), it will draw a shape like this:

Hint

The measure of the exterior angle of a regular polygon is 360 / n, so your turtle should turn left by this amount after each side.
Write a non-fruitful function draw_equitriangle(t, size, x, y) which calls draw_poly from the previous question to have its turtle draw a equilateral triangle.
Draw this pretty pattern.

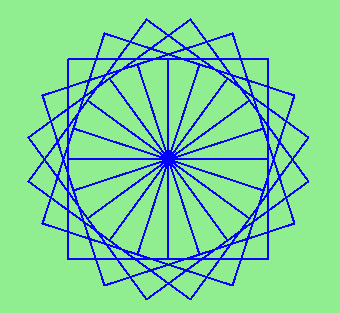
You can start by using this function:
```
def draw4squares(t, size):
    for i in range(4):
        for i in range(3):
            t.forward(size)
            t.left(90)
        t.forward(size)
```
to draws this:

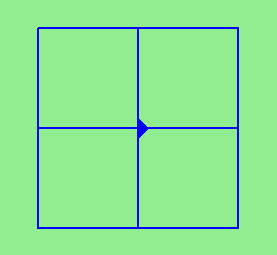
Then use another loop in the main body of your program to call draw4squares, turning the turtle each time the loop executes.

When one loop is placed inside the body of another, we say that the inner loop is a nested loop.

How many times does the statement t.forward(size) execute in a single call to draw4squares? If draw4squares is called 5 times in the main body of the program, how many times will t.forward(size) be executed?

When the function draw4squares is called inside the body of a loop, the outer loop of the function effectively becomes nested inside the loop in which the function is called, and the function’s inner loop becomes doubly nested.

By wrapping the two inner loops inside a function, we use abstraction to hide the complexity of our solution (a loop inside a loop inside a loop) from ourselves – thus keeping our heads from exploding. Abstraction is a wonderful thing!
The two spirals in this picture differ only by the turn angle. Draw both.
In the exercises in chapter 2 we were introduced to doctest and asked make doctests pass that were written at the top of a module.

Each function we define can have its own docstring, and these docstrings can hold doctests specifically for that function. In this and the next several exercises you will be asked to write the body of a function to make its doctests pass.

Create a file named ch04doctest_ex.py containing the following:
```
def h(x):
    """
      >>> h(0)
      -5
      >>> h(1)
      -3
      >>> h(3)
      1
    """

if __name__ == '__main__':
    import doctest
    doctest.testmod()
```
Write a function body for h that will make the doctests pass.

Hint

To help get you started with this process, doctests for the functions f and g from the chapter are included in ch04doctests.py.

Run this program as is and notice the error messages. Then replace the comments after the doctests for each function with the return statements given in the chapter and run the program again.

Add the following function definition header and doctests to ch04doctest_ex.py, after the definition of h(x) but before the if __name__... section at the end of the file:

def f2(x):
    """
      >>> f2(0)
      -11
      >>> f2(1)
      -6
      >>> f2(2)
      -1
      >>> f2(4)
      9
      >>> f2(-1)
      -16
    """

Repeat the process you used in the previous exercise with this new function.

def f3(x):
    """
      >>> f3(0)
      8
      >>> f3(1)
      6
      >>> f3(3)
      2
      >>> f3(-1)
      10
    """

And again with this quadratic function.

def f4(x):
    """
      >>> f4(0)
      -10
      >>> f4(1)
      -9
      >>> f4(-1)
      -9
      >>> f4(2)
      -6
      >>> f4(-2)
      -6
      >>> f4(3)
      -1
      >>> f4(5)
      15
    """

In this exercise and the one that follows, you are asked to write functions to convert temperatures between Fahrenheit and Celsius, which result in floating-point values.

Binary floating-point numbers are complex, and we don’t expect you to understand how they work at this point in your study. You should just think of them as approximations of real number values.

Python’s built-in round function converts a floating-point value into the nearest integer value:
```
>>> f = 2/3
>>> f
0.6666666666666666
>>> round(f)
1
```
You will use round in these two exercises.

Add the following function definition header and doctests to ch04doctest_ex.py:
```
def f2c(t):
    """
      >>> f2c(212)
      100
      >>> f2c(32)
      0
      >>> f2c(-40)
      -40
      >>> f2c(36)
      2
      >>> f2c(37)
      3
      >>> f2c(38)
      3
      >>> f2c(39)
      4
    """
```
Write a body for the function definition of f2c designed to return the integer value of the nearest degree Celsius for given temperature in Fahrenheit.

Add the following function definition header and doctests to ch04doctest_ex.py:

def c2f(t):
    """
      >>> c2f(0)
      32
      >>> c2f(100)
      212
      >>> c2f(-40)
      -40
      >>> c2f(12)
      54
      >>> c2f(18)
      64
      >>> c2f(-48)
      -54
    """

Add a function body for c2f to convert from Celsius to Fahrenheit.

Now add the following function header for the fruitful function sum_to(n) that returns the sum of all integer numbers up to and including n.

def sum_to(n):
    """
      >>> sum_to(0)
      0
      >>> sum_to(1)
      1
      >>> sum_to(2)
      3
      >>> sum_to(4)
      10
      >>> sum_to(10)
      55
    """

Hint

Look back over the range function introduced in the last chapter before attempting to do this exercise.

In an exercise last chapter you wrote a program to draw a star shape like this

Wrap this code in a functioned named draw_star.
Extend your program above. Add parameters for the x and y location where the star should be drawn. Use your new version to draw five stars, so you get something like this:

What would it look like if you didn’t pick up the pen?