4. Conditionals

4.1. The modulus operator

The modulus operator works on integers (and integer expressions) and yields the remainder when the first operand is divided by the second. In Python, the modulus operator is a percent sign (%). The syntax is the same as for other operators:

>>> quotient = 7 / 3
>>> print quotient
2
>>> remainder = 7 % 3
>>> print remainder
1

So 7 divided by 3 is 2 with 1 left over.

The modulus operator turns out to be surprisingly useful. For example, you can check whether one number is divisible by another—if x % y is zero, then x is divisible by y.

Also, you can extract the right-most digit or digits from a number. For example, x % 10 yields the right-most digit of x (in base 10). Similarly x % 100 yields the last two digits.

4.2. Boolean values and expressions

The Python type for storing true and false values is called bool, named after the British mathematician, George Boole. George Boole created Boolean algebra, which is the basis of all modern computer arithmetic.

There are only two boolean values: True and False. Capitalization is important, since true and false are not boolean values.

>>> type(True)
<type 'bool'>
>>> type(true)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'true' is not defined

A boolean expression is an expression that evaluates to a boolean value. The operator == compares two values and produces a boolean value:

>>> 5 == 5
True
>>> 5 == 6
False

In the first statement, the two operands are equal, so the expression evaluates to True; in the second statement, 5 is not equal to 6, so we get False.

The == operator is one of the comparison operators; the others are:

x != y               # x is not equal to y
x > y                # x is greater than y
x < y                # x is less than y
x >= y               # x is greater than or equal to y
x <= y               # x is less than or equal to y

Although these operations are probably familiar to you, the Python symbols are different from the mathematical symbols. A common error is to use a single equal sign (=) instead of a double equal sign (==). Remember that = is an assignment operator and == is a comparison operator. Also, there is no such thing as =< or =>.

4.3. Logical operators

There are three logical operators: and, or, and not. The semantics (meaning) of these operators is similar to their meaning in English. For example, x > 0 and x < 10 is true only if x is greater than 0 and less than 10.

n % 2 == 0 or n % 3 == 0 is true if either of the conditions is true, that is, if the number is divisible by 2 or 3.

Finally, the not operator negates a boolean expression, so not(x > y) is true if (x > y) is false, that is, if x is less than or equal to y.

4.4. Conditional execution

In order to write useful programs, we almost always need the ability to check conditions and change the behavior of the program accordingly. Conditional statements give us this ability. The simplest form is the ** if statement**:

if x > 0:
    print "x is positive"

The boolean expression after the if statement is called the condition. If it is true, then the indented statement gets executed. If not, nothing happens.

The syntax for an if statement looks like this:

if BOOLEAN EXPRESSION:
    STATEMENTS

As with the function definition from last chapter and other compound statements, the if statement consists of a header and a body. The header begins with the keyword if followed by a boolean expression and ends with a colon (:).

The indented statements that follow are called a block. The first unindented statement marks the end of the block. A statement block inside a compound statement is called the body of the statement.

Each of the statements inside the body are executed in order if the boolean expression evaluates to True. The entire block is skipped if the boolean expression evaluates to False.

There is no limit on the number of statements that can appear in the body of an if statement, but there has to be at least one. Occasionally, it is useful to have a body with no statements (usually as a place keeper for code you haven’t written yet). In that case, you can use the pass statement, which does nothing.

if True:          # This is always true
    pass          # so this is always executed, but it does nothing

4.5. Alternative execution

A second form of the if statement is alternative execution, in which there are two possibilities and the condition determines which one gets executed. The syntax looks like this:

if x % 2 == 0:
    print x, "is even"
else:
    print x, "is odd"

If the remainder when x is divided by 2 is 0, then we know that x is even, and the program displays a message to that effect. If the condition is false, the second set of statements is executed. Since the condition must be true or false, exactly one of the alternatives will be executed. The alternatives are called branches, because they are branches in the flow of execution.

As an aside, if you need to check the parity (evenness or oddness) of numbers often, you might wrap this code in a function:

def print_parity(x):
    if x % 2 == 0:
        print x, "is even"
    else:
        print x, "is odd"

For any value of x, print_parity displays an appropriate message. When you call it, you can provide any integer expression as an argument.

>>> print_parity(17)
17 is odd.
>>> y = 41
>>> print_parity(y+1)
42 is even.

4.6. Chained conditionals

Sometimes there are more than two possibilities and we need more than two branches. One way to express a computation like that is a chained conditional:

if x < y:
    print x, "is less than", y
elif x > y:
    print x, "is greater than", y
else:
    print x, "and", y, "are equal"

elif is an abbreviation of else if . Again, exactly one branch will be executed. There is no limit of the number of elif statements but only a single (and optional) else statement is allowed and it must be the last branch in the statement:

if choice == 'a':
    function_a()
elif choice == 'b':
    function_b()
elif choice == 'c':
    function_c()
else:
    print "Invalid choice."

Each condition is checked in order. If the first is false, the next is checked, and so on. If one of them is true, the corresponding branch executes, and the statement ends. Even if more than one condition is true, only the first true branch executes.

4.7. Nested conditionals

One conditional can also be nested within another. We could have written the trichotomy example as follows:

if x == y:
    print x, "and", y, "are equal"
else:
    if x < y:
        print x, "is less than", y
    else:
        print x, "is greater than", y

The outer conditional contains two branches. The first branch contains a simple output statement. The second branch contains another if statement, which has two branches of its own. Those two branches are both output statements, although they could have been conditional statements as well.

Although the indentation of the statements makes the structure apparent, nested conditionals become difficult to read very quickly. In general, it is a good idea to avoid them when you can.

Logical operators often provide a way to simplify nested conditional statements. For example, we can rewrite the following code using a single conditional:

if 0 < x:
    if x < 10:
        print "x is a positive single digit."

The print statement is executed only if we make it past both the conditionals, so we can use the and operator:

if 0 < x and x < 10:
    print "x is a positive single digit."

These kinds of conditions are common, so Python provides an alternative syntax that is similar to mathematical notation:

if 0 < x < 10:
    print "x is a positive single digit."

This condition is semantically the same as the compound boolean expression and the nested conditional.

4.8. The return statement

The return statement allows you to terminate the execution of a function before you reach the end. One reason to use it is if you detect an error condition:

def print_square_root(x):
    if x <= 0:
        print "Positive numbers only, please."
        return

    result = x**0.5
    print "The square root of", x, "is", result

The function print_square_root has a parameter named x. The first thing it does is check whether x is less than or equal to 0, in which case it displays an error message and then uses return to exit the function. The flow of execution immediately returns to the caller, and the remaining lines of the function are not executed.

4.9. Keyboard input

In Input we were introduced to Python’s built-in functions that get input from the keyboard: raw_input and input. Now let’s look at these again in greater depth.

When either of these functions are called, the program stops and waits for the user to type something. When the user presses Return or the Enter key, the program resumes and raw_input returns what the user typed as a string:

>>> my_input = raw_input()
What are you waiting for?
>>> print my_input
What are you waiting for?

Before calling raw_input, it is a good idea to print a message telling the user what to input. This message is called a prompt. We can supply a prompt as an argument to raw_input:

>>> name = raw_input("What...is your name? ")
What...is your name? Arthur, King of the Britons!
>>> print name
Arthur, King of the Britons!

Notice that the prompt is a string, so it must be enclosed in quotation marks.

If we expect the response to be an integer, we can use the input function which evaluates the response as a Python expression:

prompt = "What...is the airspeed velocity of an unladen swallow?\n"
speed = input(prompt)

If the user types a string of digits, it is converted to an integer and assigned to speed. Unfortunately, if the user types characters that do not make up a valid Python expression, the program crashes:

>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
What do you mean, an African or a European swallow?
...
SyntaxError: invalid syntax

In the last example, if the user had made the response a valid Python expression by putting quotes around it, it would not have given an error:

>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
"What do you mean, an African or a European swallow?"
>>> speed
'What do you mean, an African or a European swallow?'
>>>

To avoid this kind of error, it is a good idea to use raw_input to get a string and then use conversion commands to convert it to other types.

4.10. Type conversion

Each Python type comes with a built-in command that attempts to convert values of another type into that type. The int(ARGUMENT) command, for example, takes any value and converts it to an integer, if possible, or complains otherwise:

>>> int("32")
32
>>> int("Hello")
ValueError: invalid literal for int() with base 10: 'Hello'

int can also convert floating-point values to integers, but remember that it truncates the fractional part:

>>> int(-2.3)
-2
>>> int(3.99999)
3
>>> int("42")
42
>>> int(1.0)
1

The float(ARGUMENT) command converts integers and strings to floating-point numbers:

>>> float(32)
32.0
>>> float("3.14159")
3.14159
>>> float(1)
1.0

It may seem odd that Python distinguishes the integer value 1 from the floating-point value 1.0. They may represent the same number, but they belong to different types. The reason is that they are represented differently inside the computer.

The str(ARGUMENT) command converts any argument given to it to type string:

>>> str(32)
'32'
>>> str(3.14149)
'3.14149'
>>> str(True)
'True'
>>> str(true)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'true' is not defined

str(ARGUMENT) will work with any value and convert it into a string. As mentioned earlier, True is boolean value; true is not.

For boolean values, the situation is especially interesting:

>>> bool(1)
True
>>> bool(0)
False
>>> bool("Ni!")
True
>>> bool("")
False
>>> bool(3.14159)
True
>>> bool(0.0)
False

Python assigns boolean values to values of other types. For numerical types like integers and floating-points, zero values are false and non-zero values are true. For strings, empty strings are false and non-empty strings are true.

4.11. GASP

GASP (Graphics API for Students of Python) will enable us to write programs involving graphics. Before you can use GASP, it needs to be installed on your machine. If you are running Ubuntu GNU/Linux, see GASP in Appendix A. Current instructions for installing GASP on other platforms can be found at http://dev.laptop.org/pub/gasp/downloads.

After installing gasp, try the following python script:

from gasp import *

begin_graphics()

Circle((200, 200), 60)
Line((100, 400), (580, 200))
Box((400, 350), 120, 100)

update_when('key_pressed')
end_graphics()

The second to the last command pauses and waits until a key is pressed. Without it, the screen would flash by so quickly you wouldn’t see it.

Running this script, you should see a graphics window that looks like this:

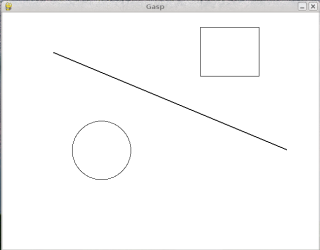
We will be using gasp from here on to illustrate (pun intended) computer programming concepts and to add to our fun while learning. You can find out more about the GASP module by reading Appendix B.

4.12. Glossary

block

A group of consecutive statements with the same indentation.

body

The block of statements in a compound statement that follows the header.

boolean expression

An expression that is either true or false.

boolean value

There are exactly two boolean values: True and False. Boolean values result when a boolean expression is evaluated by the Python interepreter. They have type bool.

branch

One of the possible paths of the flow of execution determined by conditional execution.

chained conditional

A conditional branch with more than two possible flows of execution. In Python chained conditionals are written with if ... elif ... else statements.

comparison operator

One of the operators that compares two values: ==, !=, >, <, >=, and <=.

condition

The boolean expression in a conditional statement that determines which branch is executed.

conditional statement

A statement that controls the flow of execution depending on some condition. In Python the keywords if, elif, and else are used for conditional statements.

logical operator

One of the operators that combines boolean expressions: and, or, and not.

modulus operator

An operator, denoted with a percent sign ( %), that works on integers and yields the remainder when one number is divided by another.

nesting

One program structure within another, such as a conditional statement inside a branch of another conditional statement.

prompt

A visual cue that tells the user to input data.

type conversion

An explicit statement that takes a value of one type and computes a corresponding value of another type.

wrapping code in a function

The process of adding a function header and parameters to a sequence of program statements is often refered to as “wrapping the code in a function”. This process is very useful whenever the program statements in question are going to be used multiple times.

4.13. Exercises

1. Try to evaluate the following numerical expressions in your head, then use the Python interpreter to check your results:

   1. >>> 5 % 2
   2. >>> 9 % 5
   3. >>> 15 % 12
   4. >>> 12 % 15
   5. >>> 6 % 6
   6. >>> 0 % 7
   7. >>> 7 % 0

   What happened with the last example? Why? If you were able to correctly anticipate the computer’s response in all but the last one, it is time to move on. If not, take time now to make up examples of your own. Explore the modulus operator until you are confident you understand how it works.

2. if x < y:
       print x, "is less than", y
   elif x > y:
       print x, "is greater than", y
   else:
       print x, "and", y, "are equal"
   

   Wrap this code in a function called compare(x, y). Call compare three times: one each where the first argument is less than, greater than, and equal to the second argument.

3. To better understand boolean expressions, it is helpful to construct truth tables. Two boolean expressions are logically equivalent if and only if they have the same truth table.

   The following Python script prints out the truth table for any boolean expression in two variables: p and q:

   expression = raw_input("Enter a boolean expression in two variables, p and q: ")
   
   print " p      q      %s"  % expression
   length = len( " p      q      %s"  % expression)
   print length*"="
   
   for p in True, False:
       for q in True, False:
           print "%-7s %-7s %-7s" % (p, q, eval(expression))
   

   You will learn how this script works in later chapters. For now, you will use it to learn about boolean expressions. Copy this program to a file named p_and_q.py, then run it from the command line and give it: p or q, when prompted for a boolean expression. You should get the following output:

    p      q      p or q
   =====================
   True    True    True
   True    False   True
   False   True    True
   False   False   False
   

   Now that we see how it works, let’s wrap it in a function to make it easier to use:

   def truth_table(expression):
       print " p      q      %s"  % expression
       length = len( " p      q      %s"  % expression)
       print length*"="
   
       for p in True, False:
           for q in True, False:
               print "%-7s %-7s %-7s" % (p, q, eval(expression))
   

   We can import it into a Python shell and call truth_table with a string containing our boolean expression in p and q as an argument:

   >>> from p_and_q import *
   >>> truth_table("p or q")
   p      q      p or q
   =====================
   True    True    True
   True    False   True
   False   True    True
   False   False   False
   >>>
   

   Use the truth_table functions with the following boolean expressions, recording the truth table produced each time:

   1. not(p or q)
   2. p and q
   3. not(p and q)
   4. not(p) or not(q)
   5. not(p) and not(q)

   Which of these are logically equivalent?

4. Enter the following expressions into the Python shell:

   True or False
   True and False
   not(False) and True
   True or 7
   False or 7
   True and 0
   False or 8
   "happy" and "sad"
   "happy" or "sad"
   "" and "sad"
   "happy" and ""
   

   Analyze these results. What observations can you make about values of different types and logical operators? Can you write these observations in the form of simple rules about and and or expressions?

5. if choice == 'a':
       function_a()
   elif choice == 'b':
       function_b()
   elif choice == 'c':
       function_c()
   else:
       print "Invalid choice."
   

   Wrap this code in a function called dispatch(choice). Then define function_a, function_b, and function_c so that they print out a message saying they were called. For example:

   def function_a():
       print "function_a was called..."
   

   Put the four functions ( dispatch, function_a, function_b, and function_c into a script named ch04e05.py. At the bottom of this script add a call to dispatch('b'). Your output should be:

   function_b was called...
   

   Finally, modify the script so that user can enter ‘a’, ‘b’, or ‘c’. Test it by importing your script into the Python shell.

6. Write a function named is_divisible_by_3 that takes a single integer as an argument and prints “This number is divisible by three.” if the argument is evenly divisible by 3 and “This number is not divisible by three.” otherwise.

   Now write a similar function named is_divisible_by_5.

7. Generalize the functions you wrote in the previous exercise into a function named is_divisible_by_n(x, n) that takes two integer arguments and prints out whether the first is divisible by the second. Save this in a file named ch04e07.py. Import it into a shell and try it out. A sample session might look like this:

   >>> from ch04e07 import *
   >>> is_divisible_by_n(20, 4)
   Yes, 20 is divisible by 4
   >>> is_divisible_by_n(21, 8)
   No, 21 is not divisible by 8
   

8. What will be the output of the following?

   if "Ni!":
       print 'We are the Knights who say, "Ni!"'
   else:
       print "Stop it! No more of this!"
   
   if 0:
       print "And now for something completely different..."
   else:
       print "What's all this, then?"
   

   Explain what happened and why it happened.

9. The following gasp script, in a file named house.py, draws a simple house on a gasp canvas:

   from gasp import *          # import everything from the gasp library
   
   begin_graphics()            # open the graphics canvas
   
   Box((20, 20), 100, 100)     # the house
   Box((55, 20), 30, 50)       # the door
   Box((40, 80), 20, 20)       # the left window
   Box((80, 80), 20, 20)       # the right window
   Line((20, 120), (70, 160))  # the left roof
   Line((70, 160), (120, 120)) # the right roof
   
   update_when('key_pressed')  # keep the canvas open until a key is pressed
   end_graphics()              # close the canvas (which would happen
                               # anyway, since the script ends here, but it
                               # is better to be explicit).
   

   Run this script and confirm that you get a window that looks like this:

   
   1. Wrap the house code in a function named draw_house().
   2. Run the script now. Do you see a house? Why not?
   3. Add a call to draw_house() at the botton of the script so that the house returns to the screen.
   4. Parameterize the function with x and y parameters – the header should then become def draw_house(x, y):, so that you can pass in the location of the house on the canvas.
   5. Use draw_house to place five houses on the canvas in different locations.

10. Exploration: Read over Appendix B and write a script named houses.py that produces the following when run:

    

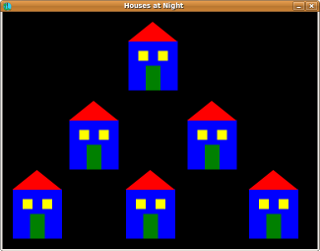
    hint: You will need to use a Polygon for the roof instead of two Lines to get filled=True to work with it.