Wealth inequality grows

In the November edition of Scientific American was an article titled "Is Inequality Inevitable?". The author, Bruce Boghosian, is a math professor at Tufts Univerisity and he makes a good case for how wealth trickles up to the top pretty much automatically.

As an example he uses a coin flip that wins you 20% if you win and costs you just 17% if you lose. So if put down $100, and then the coin is flipped. If it comes up heads your opponent adds $20 to your $100. If the coin come up tails, then $17 dollars comes off your pile and onto his. You may both continue as long as you want. Each time you win the flip, your stake grows 20%. Each time you 17% comes off.

In a series of flips you would probably expect that the money on the table would grow over time. But this is not the case. Here's why. If you lose the first flip you have $83 on the table. If you then win the second flip you might expect that you now have $103. But instead you have $99.60!

Because 20% of $83 doesn't cover the loss.

And if you win the first flip, leaving you with $120 on the table, but then lose the second flip you also have $99.60. 17% of $120 is slighty more than $20.

No real magic here. Both yield the same result simply because "x*y" is equal to "y*x".

The calulations for the two scenarios are

(100+20)*0.83  is 99.60 - win then loss
(100-17)*1.20  is 99.60 - loss then win

So, you are 40 cents down either way.

Now, this might be disturbing. If both you and your opponent have the same stake, you can't both be down 40 cents. And you won't. With each flip the bet is based on 20/17 of the smaller pile. If your opponent has a much bigger pile than you, then the size of the bet is always based on your pile. Let's assume your opponent initally put up $1000.

         you                             opponent
init   $100.00                           $1000.00
loss   $ 83.00  down 17% of $100         $1017.00
win    $ 99.60  up   20% of $ 83         $1000.40

Playing multiple games

Let's play 10 games with 20 flips in each game. You might win anywhere from zero to 10 games but the extremes are unlikely. Here a table of some results and your standing at the end. The first column adds to 10 and is the number of games that come up with the same number of heads in the second column.

1 006 heads in 20 flips $  21.99
1 008 heads in 20 flips $  45.96
3 009 heads in 20 flips $  66.45
2 010 heads in 20 flips $  96.07
1 011 heads in 20 flips $ 138.90
1 012 heads in 20 flips $ 200.82
1 013 heads in 20 flips $ 290.34

Right in the middle, if you win 10 times out of 20 flips, you end up with 96.07 which is just a rounding error away from ten times the 40 cents above.

Group playing

Another scenario that is described in the article involves multiple players each starting out with $100 and playing randomly with each other, always using the smaller balance to set the size of the bet. In the plots below each player is represented by a certain color. It's interesting to see the chaos as the playing proceeds. But notice how one player, Diane, has almost all the money after 1000 transactions.

$ python group.py  trades=1000 seed=8623
rates 0.2 0.17
  437.39  Diane    orange
  133.70  Betty    green
   28.41  Erica    yellow
    0.48  Alan     red
    0.02  Charlie  blue
    0.00  Frank    purple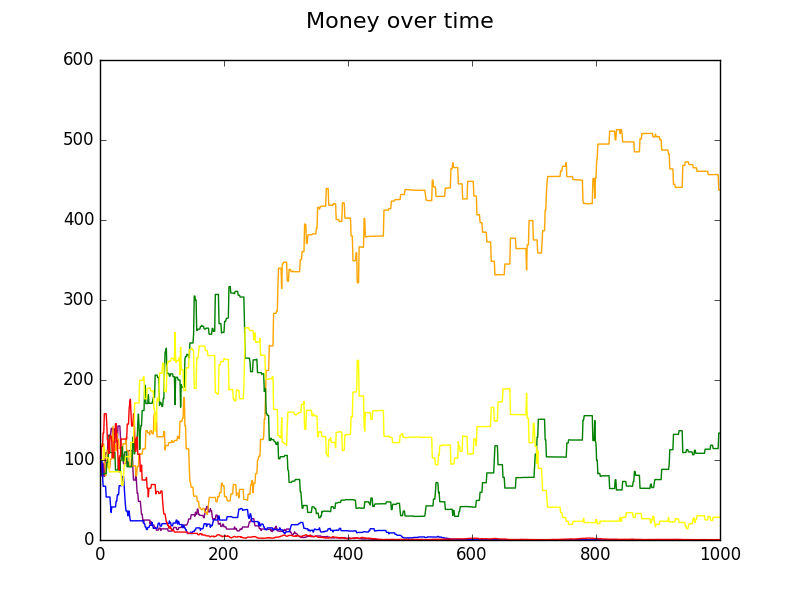

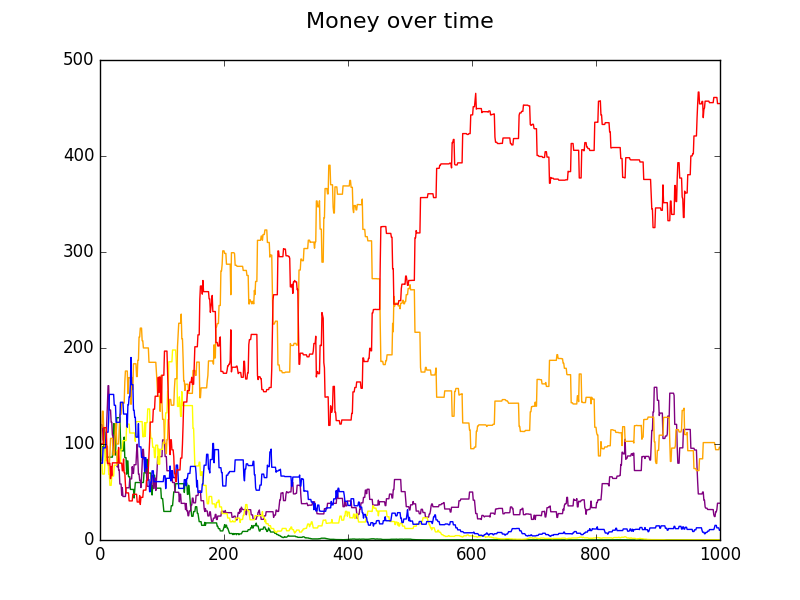
Next we show two plots of the same sequence of wins (seeding the random number generator) for both 500 and 1000 flips. You can see how the inequality keeps increasing over time.

$ python group.py  trades=500  seed=3795
rates 0.2 0.17
  270.35  Alan     red
  265.92  Diane    orange
   31.30  Frank    purple
   19.57  Charlie  blue
   12.00  Erica    yellow
    0.86  Betty    green

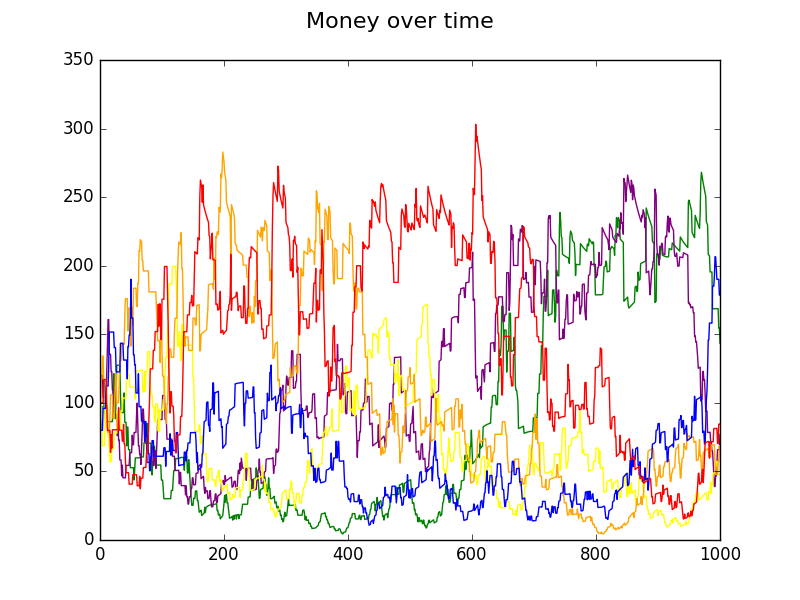
$ python group.py  trades=1000  seed=3795
rates 0.2 0.17
  454.61  Alan     red
   96.64  Diane    orange
   38.32  Frank    purple
   10.11  Charlie  blue
    0.24  Erica    yellow
    0.08  Betty    green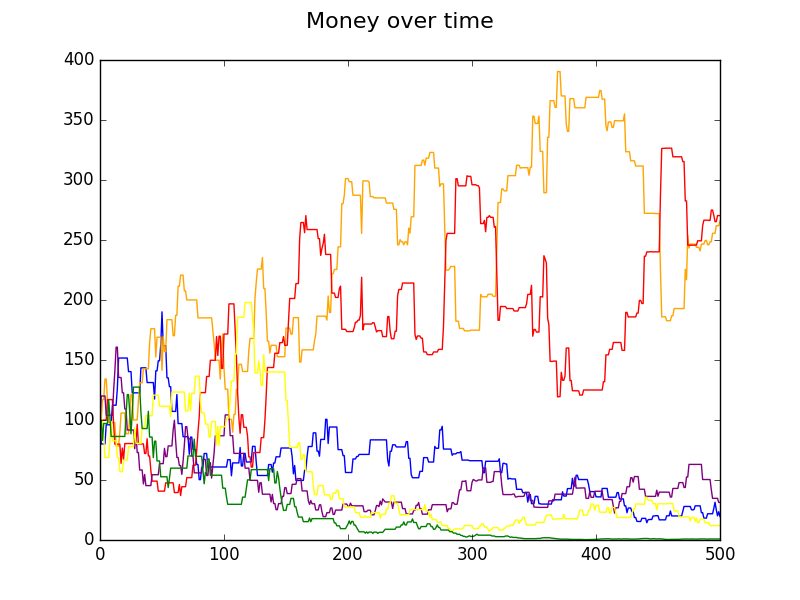

What about a wealth tax

A wealth tax is often mentioned as a way to put a brake on this natural upflow of money. Here we simulate a 5% tax on wealth over $200. The tax collected is then spread evenly over all players (including the one taxed).

There are two plots. The first with 500 flips, and the second 1000. The game is still pretty chaotic. But notice how Charlie in blue came from the bottom in the first 500 flips to the top in the next 500. Peak wealth is held at just under $300.

$ python group.py  trades=500  seed=3795 taxRate=.05
rates 0.2 0.17
  228.41  Alan     red
  125.66  Diane    orange
   99.63  Erica    yellow
   72.08  Frank    purple
   43.75  Betty    green
   30.48  Charlie  blue

$ python group.py  trades=1000  seed=3795 taxRate=.05
rates 0.2 0.17
  178.59  Charlie  blue
  143.42  Betty    green
   84.48  Alan     red
   77.01  Frank    purple
   68.76  Diane    orange
   47.75  Erica    yellow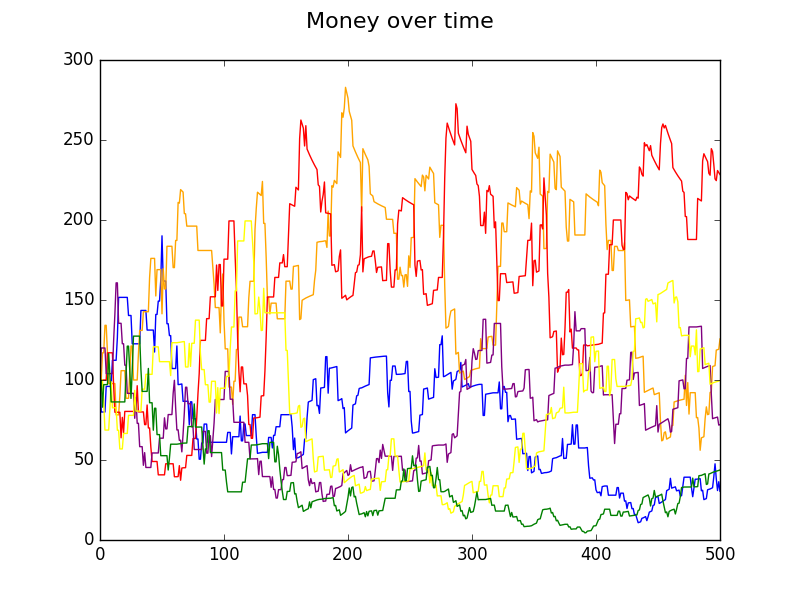

The program itself

The class Player is used only to supply attributes for each player. There are no methods in the class. the players name, and money are obvious. color and hist are kept for making the plots.

Python's random number generator supplies the "heads" and "tails" calls. The function flipcoin takes 2 players and the win/loss rates. Even odds for heads or tails (line 10) and then the money is adjusted for each player. The function returns True if it was heads or False if tails.

The function randomSeed gives us the option to seed the random number generator. This lets us reproduce earlier runs of the program. A value like "seed=1234" may be passed on the command line. If it's not then randomSeed will choose a seed on its own and print the seed so that you can reuse the future runs.

Here is a listing of common.py that contains these features.

03 import random, sarg
04
05 class Player :
06     def __init__ (s, name, color, money=100.0) :
07         s.name = name; s.color=color; s.money=money; s.hist=[money]
08
09 def flipCoin (player1, player2, winRate, lossRate) :
10         heads = (random.random() >= .5)
11         amt = min(player1.money, player2.money)
12         if heads :
13             player1.money += amt*winRate
14             player2.money -= amt*winRate
15         else :
16             player1.money -= amt*lossRate
17             player2.money += amt*lossRate
18         return heads
19
20 def randomSeed() :
21     seed = sarg.Int("seed",0)
22     if seed == 0 :
23         seed = int(random.random()*10000)  # choose a seed
24         print "--- seed=%d !" % seed
25     random.seed(seed)

You might notice on line 21 a call that picks up a seed for the random number generator from the command line. Documentation for sarg.py (simple arguments) can be found in the pglib project

The following listing contains the group playing program above. We'll explain it in chunks but since we have already seen it run, the code should be quite understandable.

01 #!/usr/local/bin/python
02 #
03 #  group.py
04 #
05 import random, sarg
06 from   common import Player, flipCoin, randomSeed
07
08 names = ['Alan', 'Betty', 'Charlie', 'Diane', 'Erica', 'Frank']
09 colors= [ 'red', 'green',    'blue','orange','yellow', 'purple']
10
11 def groupPlay() :
12     players = [Player(names[i],colors[i]) for i in range(len(names))]

The array players contains the 5 players. Their names and colors are assigned here. They are automatically given $100 to start

13     winRate  = sarg.Float("winRate", .20) # fraction player gets for win
14     lossRate = sarg.Float("lossRate",.17) # fraction player pays for loss
15     taxRate  = sarg.Float("taxRate", .00) # tax over $200 each transaction
16     print "rates", winRate, lossRate
17

The sarg module picks up the variables for the run from the command line or just uses the default in the second argument.

18     for j in range(sarg.Int("trades",500)):
19         random.shuffle(players)
20         isHeads = flipCoin(players[0], players[1], winRate, lossRate)
21         wealthTax(players, taxRate)
22         for player in players :   # for each player
23             player.hist.append(round(player.money,2))

The for loop at line 18 handles the tradeing. The players are shuffled like cards, and the top two flip the coin. If there is a wealth tax it's applied. The for loop at line 22 saves the money history for each player.

24     ranking = [(p.money, p) for p in players]
25     ranking.sort()
26     for bal,player in reversed(ranking) :
27         print "%8.02f  %-8s %s" % (bal, player.name, player.color)
28     plotMoney(players)

Finally, the players are sorted by wealth with the richest at the top. This is then printed as we saw above and then plotted.

29
30 def wealthTax(players,taxRate) :
31     # if wealth exceed 200, tax the excess at the taxRate
32     totTax = 0.0
33     for player in players :
34         tax = max(0., player.money-200)*taxRate
35         totTax += tax
36         player.money -= tax
37     dist = totTax/len(players)    # spread evenly to all players
38     for player in players : player.money += dist

The wealth tax may be applied if specified in the command but the default is zero. The rich are taxed at line 34 and the proceeds distributed in line 38.

39
40 def plotMoney(players) :
41     import matplotlib.pyplot as plt
42     plt.suptitle("Money over time", size=16)
43     for player in players :
44         xps = list(range(len(player.hist)))
45         yps = player.hist
46         plt.plot(xps,yps, player.color)
47     plt.show()

I won't go into detail on the plotting. Each player is drawn in its color with lines connecting one history point to the next. Good documentation on matplotlib is available on the web.

48
49 if __name__ == "__main__" :
50     randomSeed()
51     groupPlay()

And finally, the program is kicked off. You can download the above code here

If you have comments or suggestions You can email me at mail me

* * *