The Tower of Hanoi: Recursion with Animation

The Tower of Hanoi is a classic game that is often emulated on computers to demonstrate recursion.

The game runs as follows. There are a number of discs each with a hole in the center. Each disc can fit on any of 3 pegs and each peg is high enough to hold all the discs in a stack. In the initial configuration all the discs are stacked on the first peg with the largest disc on the bottom and the smallest on top. A disc is never stacked on top of a smaller disc. The problem is to move the discs, one at a time from peg to peg in such a way that this is always true and to finally end up with all of the discs on peg 3 in the original order.

The solution is elegant. Let's call the three pegs A, B, and C. If you don't know how to move 5 discs from A to C (using B for intermediate storage), then just move 4 discs from A to B, one disk from A to C (this is really easy) and then move 4 discs from B to C. Can't do 4 discs? Well then, move just 3 ...

Guido's hanoi.py in the Python Demo area is a nice demonstration of this recursive process. The heart of the program is just this.

def hanoi(n, a, b, c, report):
   if n <= 0: return
   hanoi(n-1, a, c, b, report)
   report(n, a, b)
   hanoi(n-1, c, b, a, report)
-

The other 99% of the program involves doing TK graphics to make it come alive. Here is a screen shot of the game in progress.

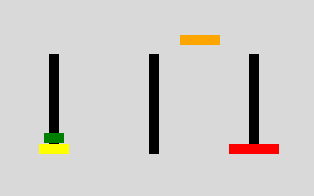
And here is a javascript animation . Use browser back-button to return.

I have tried a couple of times to teach the Hanoi puzzle as a good example of recursion. It is much better than the usual factorial example which does nothing more than use recursion to replace a simple for loop.

But students have a hard time getting it. And I think the problem is the difficulty in visualizing the nested context of the recursive calls. We’ll take it on slowly.

Model View and Controller

The MVC discipline strives to find separate responsibilities of a program into code modules that are independent and loosely linked with each other.

The Model is a structure for the data being manipulated by the program

The Control is makes changes to the contents of the model and also passes the changing model along with other signals to the view.

The View outputs the model, either presenting a visual repretation, outputting information from the model, responding to signals from the Control or all of these. Some applications may have multiple views.

The Model

In the Tower of Hanoi an object oriented model might consist of a class for a disc and another for a peg. Each disc might have attributes for its size and color along with which peg it is stacked. A peg object might have attributes for its position and which disc objects are attached to it. Along with the attributes might be methods to move a disc from peg to peg and to calculate which disc and which peg should be next.

But this model would be fairly involved. In this project we use a much simpler model, a list structure. This list has an entry for each peg. Each peg would also be a list with an integer for each disc. The discs sorted by size top to bottom (small to large) on the peg. At the start the model looks like the following with all discs stacked on the first peg (peg 0).

 [ [1,2,3,4], [], [] ]

The Control

The control for the Tower of Hanoi will turn out be quite simple but tricky. We’ll use the simple version of the model and the initial view will simply print the model. That’s easy since it’s just a Python expression and the python print statement works fine. We won’t bother with separate module for it.

As we do in many of the projects, we want to start by finding a solution for the simplest case. If we need to move just one disc, it’s just a single step: move the disc from the source peg to the destination peg. Pop it off the source peg and append it to the destination peg. That can be done in a single statement.

For two discs (2-discs) we can invoke the 1-disc code three times: move the top (smallest) disc to the auxillary peg, then move the next to the destination peg. And finally move the disc on the auxillary peg to the destination peg. Done.

And with that solution we can make a 3-disc solution. 2-disc to the auxillary peg, 1-disc to the destination and 2-disc again to move discs from the auxillary peg to the destination peg. Done.

And with a 3-disc solution a 4-disc can be … I’m sure you have the idea.

Here’s our first attempt at some control code. A much better one will follow in bit. We are going to avoid recursion by limiting the number of disks and writing a separate function for each case.

code for hanoiNR.py

model = [[1,2,3,4],[],[]]   # A simple model, a list with 3 pegs each with up to 4 discs

def move1(src,dest) :
    print("move disk from %s to %s" % (src,dest))
    model[dest].append(model[src].pop())           # move top disc on src to top of dest
    
def move2(src,dest, aux) :
    move1(src,aux)
    move1(src,dest)
    move1(aux,dest)

def move3(src,dest, aux) :
    move2(src,aux,  dest)
    move1(src,dest)
    move2(aux,dest, src)

def move4(src,dest, aux) :
    move3(src,aux,  dest)
    move1(src,dest)
    move3(aux,dest, src)

And this is what we get when it is run

$ python hanoiNR.py 
[[1, 2, 3, 4], [], []]
move disk from 0 to 2
move disk from 0 to 1
move disk from 2 to 1
move disk from 0 to 2
move disk from 1 to 0
move disk from 1 to 2
move disk from 0 to 2
move disk from 0 to 1
move disk from 2 to 1
move disk from 2 to 0
move disk from 1 to 0
move disk from 2 to 1
move disk from 0 to 2
move disk from 0 to 1
move disk from 2 to 1
[[], [1, 2, 3, 4], []]

Recursion explained

When I started programming our only language (Fortran) did not support recursion. Each function had its own call frame, a workspace which was created when the program was compiled. Here the local variables including the parameters in the call were kept and manipulated. The code itself was read-only. A Fortran version of the code above worked fine with 4 discs. But for more discs more (virtually identical) functions must be created.

Recursion, which allows simultanious activations of a function, is made possible with a simple trick. Instead of the compiler creating the call frame for the function, a new call frame is created at runtime each time the function is invoked. When the function is finished and and the result returned to its caller the call frame can be discarded. There may be multiple invocations of a function each with their own call frame that can keep on going.

This is not the full story. Tail recursion reuses call frames, but that’s not an issue here

So, here is the real code for the control section. The functions move1, move2, move3 and move4 have been “folded” into a single function hanoi. The number of discs to move, ndiscs, is passed as the first parameter.

code for hanoi.py


import view

model = [[1,2,3,4],[],[]]

def hanoi(ndiscs,src,dest,aux) :
    global model
    if ndiscs == 1 :
        print("move disc from %s to %s" % (src,dest))
        print(model)
        view.moveDisc(model,src,dest)        # send signal to view code
        model[dest].append(model[src].pop()) # move disc from src to dest
    else :
        hanoi(ndiscs-1, src, aux, dest)
        hanoi(  1     , src, dest, aux)
        hanoi(ndiscs-1, aux, dest, src)

ndiscs = 4
view.init(model)                # ask view code to set up visualization
hanoi(ndiscs, 0, 2, 1)          # move stack on peg 0 to peg 2 using peg 1 as auxiallary

$ python hanoi.py

So now, instead of just printing the model, our view module that animates the discs. Let’s look at that next.

A Better View

A python structure like [ [], [1,2,3,4], [] ] makes a great model but as a view it lacks a little something. With our graphics package we can create a dynamic view that is much more interesting.

The Zelle graphics does a lot of the heavy lifting for us. We can create rectangles for pegs and discs in different sizes and colors and gently move discs from peg to peg.

Generally an animation requires us to draw each frame completely. While one frame is on the screen the next is drawn on an invisible screen in the background. If some elements in the animation are moving then they change position between frames. At the right time and when the new frame is complete the screens are swapped. If the rate is 30 times a second or faster then our brains perceive it as smooth motion.

The graphics package does this for us in the background, as far as I can tell. We simply create objects such as rectangles, polygons, text blocks and more and simply draw them, undraw them or have them move. Objects that are created later sit “above” earlier ones. When objects move they can slide over other objects they are above or under other objects without disturbing them. Nothing gets “erased” until it’s undrawn.

Our view module creates an animation very similar to the one you saw earlier. Discs and pegs are simple rectangles. The discs can move along paths that we construct. And discs are created after the pegs so that a disc can slide up and down a peg without appearing to be behind it.

The control code in hanoi.py calls the view.init function with the initial model. It is called just once. Control makes subsequent calls to view.moveDisc passing the updated model and the start and stop pegs. It is always the top disc on the source peg that is moved and it becomes the top disc at the destination.

code for view.py

Let’s look at a few of the trickier bits.

view.init creates the rectangles for the discs and pegs and draws them. In the dictionary discAttr we have the width and color of each disc (up to 4). Another dictionary stores a reference for each disc of its associated rectangle (view.drawDisc).


def init(model) :
    drawPoles()
    for peg in range(len(model)) :
        discs = model[peg]
        drawDiscs(peg, discs)

view.calcPath calculates the path for the top disc on the source peg to travel to the open area on the destination disc. It returns a reference to the disc and a triple of (steps,dx,dy) for the 3 segments of the path (up, over and down).


def calcPath(model, start, stop) :     # peg-start (0-2) to peg-stop (0-2)
    disc = model[start][-1]
    xdist = pegAttr[stop][1]-pegAttr[start][1]
    xsteps= abs(xdist);  xinc=xdist/xsteps
    yup  = pegTop(len(model[start] ))-80
    ydown= pegTop(len(model[stop])+1)-80  # plus space not there yet
    return disc, ((yup,0,-1), (xsteps,xinc,0), (ydown,0,1))

The rectangle for the disc is then moved pixel by pixel through the 3 segments of the path. After each move the program sleeps .01 seconds. Changing this will change the speed of the animation.


def moveRect(rect, amounts) :
    for steps,dx,dy in amounts :
        for i in range(steps) :
            rect.move(dx,dy)
            time.sleep(.01)

Function view.test is only run if view.py is run standalone.

The monks of Hanoi were said to play the game with 64 discs and when finished, the universe would end. How well does this jive with current cosmology? ;)

You can download this zip file for this project

If you have comments or suggestions You can email me at mail me

* * *