24. Linked lists

24.1. Embedded references

We have seen examples of attributes that refer to other objects, which we called embedded references. A common data structure, the linked list, takes advantage of this feature.

Linked lists are made up of nodes, where each node contains a reference to the next node in the list. In addition, each node contains a unit of data called the cargo.

A linked list is considered a recursive data structure because it has a recursive definition.

A linked list is either:

1. the empty list, represented by None, or
2. a node that contains a cargo object and a reference to a linked list.

Recursive data structures lend themselves to recursive methods.

24.2. The Node class

As usual when writing a new class, we’ll start with the initialization and __str__ methods so that we can test the basic mechanism of creating and displaying the new type:

class Node:
    def __init__(self, cargo=None, next=None):
        self.cargo = cargo
        self.next  = next

    def __str__(self):
        return str(self.cargo)

As usual, the parameters for the initialization method are optional. By default, both the cargo and the link, next, are set to None.

The string representation of a node is just the string representation of the cargo. Since any value can be passed to the str function, we can store any value in a list.

To test the implementation so far, we can create a Node and print it:

>>> node = Node("test")
>>> print(node)
test

To make it interesting, we need a list with more than one node:

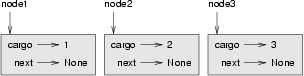
>>> node1 = Node(1)
>>> node2 = Node(2)
>>> node3 = Node(3)

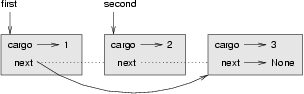
This code creates three nodes, but we don’t have a list yet because the nodes are not linked. The state diagram looks like this:

To link the nodes, we have to make the first node refer to the second and the second node refer to the third:

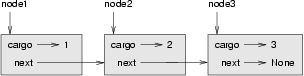
>>> node1.next = node2
>>> node2.next = node3

The reference of the third node is None, which indicates that it is the end of the list. Now the state diagram looks like this:

Now you know how to create nodes and link them into lists. What might be less clear at this point is why.

24.3. Lists as collections

Lists are useful because they provide a way to assemble multiple objects into a single entity, sometimes called a collection. In the example, the first node of the list serves as a reference to the entire list.

To pass the list as a parameter, we only have to pass a reference to the first node. For example, the function print_list takes a single node as an argument. Starting with the head of the list, it prints each node until it gets to the end:

def print_list(node):
    while node is not None:
        print(node, end=" ")
        node = node.next
    print()

To invoke this method, we pass a reference to the first node:

>>> print_list(node1)
1 2 3

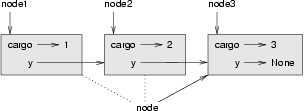
Inside print_list we have a reference to the first node of the list, but there is no variable that refers to the other nodes. We have to use the next value from each node to get to the next node.

To traverse a linked list, it is common to use a loop variable like node to refer to each of the nodes in succession.

This diagram shows the value of list and the values that node takes on:

24.4. Lists and recursion

It is natural to express many list operations using recursive methods. For example, the following is a recursive algorithm for printing a list backwards:

1. Separate the list into two pieces: the first node (called the head); and the rest (called the tail).
2. Print the tail backward.
3. Print the head.

Of course, Step 2, the recursive call, assumes that we have a way of printing a list backward. But if we assume that the recursive call works — the leap of faith — then we can convince ourselves that this algorithm works.

All we need are a base case and a way of proving that for any list, we will eventually get to the base case. Given the recursive definition of a list, a natural base case is the empty list, represented by None:

def print_backward(list):
    if list is None: return
    head = list
    tail = list.next
    print_backward(tail)
    print(head, end=" ")

The first line handles the base case by doing nothing. The next two lines split the list into head and tail. The last two lines print the list. The end argument of the print statement keeps Python from printing a newline after each node.

We invoke this method as we invoked print_list:

>>> print_backward(node1)
3 2 1

The result is a backward list.

You might wonder why print_list and print_backward are functions and not methods in the Node class. The reason is that we want to use None to represent the empty list and it is not legal to invoke a method on None. This limitation makes it awkward to write list – manipulating code in a clean object-oriented style.

Can we prove that print_backward will always terminate? In other words, will it always reach the base case? In fact, the answer is no. Some lists will make this method crash.

Revisit the Recursion chapter

In our earlier chapter on recursion we distinguished between the high-level view that requires a leap of faith, and the low-level operational view. In terms of mental chunking, we want to encourage the more abstract high-level view.

But if you’d like to see the detail you should use your single-stepping debugging tools to step into the recursive levels and to examine the execution stack frames at every call to print_backward.

24.5. Infinite lists

There is nothing to prevent a node from referring back to an earlier node in the list, including itself. For example, this figure shows a list with two nodes, one of which refers to itself:

If we invoke print_list on this list, it will loop forever. If we invoke print_backward, it will recurse infinitely. This sort of behavior makes infinite lists difficult to work with.

Nevertheless, they are occasionally useful. For example, we might represent a number as a list of digits and use an infinite list to represent a repeating fraction.

Regardless, it is problematic that we cannot prove that print_list and print_backward terminate. The best we can do is the hypothetical statement, “If the list contains no loops, then these methods will terminate.” This sort of claim is called a precondition. It imposes a constraint on one of the parameters and describes the behavior of the method if the constraint is satisfied. You will see more examples soon.

24.6. The fundamental ambiguity theorem

One part of print_backward might have raised an eyebrow:

head = list
tail = list.next

After the first assignment, head and list have the same type and the same value. So why did we create a new variable?

The reason is that the two variables play different roles. We think of head as a reference to a single node, and we think of list as a reference to the first node of a list. These roles are not part of the program; they are in the mind of the programmer.

In general we can’t tell by looking at a program what role a variable plays. This ambiguity can be useful, but it can also make programs difficult to read. We often use variable names like node and list to document how we intend to use a variable and sometimes create additional variables to disambiguate.

We could have written print_backward without head and tail, which makes it more concise but possibly less clear:

def print_backward(list):
    if list is None: return
    print_backward(list.next)
    print(list, end=" ")

Looking at the two function calls, we have to remember that print_backward treats its argument as a collection and print treats its argument as a single object.

The fundamental ambiguity theorem describes the ambiguity that is inherent in a reference to a node: A variable that refers to a node might treat the node as a single object or as the first in a list of nodes.

24.7. Modifying lists

There are two ways to modify a linked list. Obviously, we can change the cargo of one of the nodes, but the more interesting operations are the ones that add, remove, or reorder the nodes.

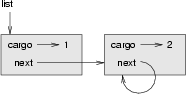
As an example, let’s write a method that removes the second node in the list and returns a reference to the removed node:

def remove_second(list):
    if list is None: return
    first = list
    second = list.next
    # Make the first node refer to the third
    first.next = second.next
    # Separate the second node from the rest of the list
    second.next = None
    return second

Again, we are using temporary variables to make the code more readable. Here is how to use this method:

>>> print_list(node1)
1 2 3
>>> removed = remove_second(node1)
>>> print_list(removed)
2
>>> print_list(node1)
1 3

This state diagram shows the effect of the operation:

What happens if you invoke this method and pass a list with only one element (a singleton)? What happens if you pass the empty list as an argument? Is there a precondition for this method? If so, fix the method to handle a violation of the precondition in a reasonable way.

24.8. Wrappers and helpers

It is often useful to divide a list operation into two methods. For example, to print a list backward in the conventional list format [3, 2, 1] we can use the print_backward method to print 3, 2, but we need a separate method to print the brackets and the first node. Let’s call it print_backward_nicely:

def print_backward_nicely(list):
    print("[", end=" ")
    print_backward(list)
    print("]")

Again, it is a good idea to check methods like this to see if they work with special cases like an empty list or a singleton.

When we use this method elsewhere in the program, we invoke print_backward_nicely directly, and it invokes print_backward on our behalf. In that sense, print_backward_nicely acts as a wrapper, and it uses print_backward as a helper.

24.9. The LinkedList class

There are some subtle problems with the way we have been implementing lists. In a reversal of cause and effect, we’ll propose an alternative implementation first and then explain what problems it solves.

First, we’ll create a new class called LinkedList. Its attributes are an integer that contains the length of the list and a reference to the first node. LinkedList objects serve as handles for manipulating lists of Node objects:

class LinkedList:
    def __init__(self):
        self.length = 0
        self.head = None

One nice thing about the LinkedList class is that it provides a natural place to put wrapper functions like print_backward_nicely, which we can make a method of the LinkedList class:

class LinkedList:
    ...
    def print_backward(self):
        print("[", end=" ")
        if self.head is not None:
            self.head.print_backward()

class Node:
    ...
    def print_backward(self):
        if self.next is not None:
            tail = self.next
            tail.print_backward()
        print(self.cargo, end=" ")

Just to make things confusing, we renamed print_backward_nicely. Now there are two methods named print_backward: one in the Node class (the helper); and one in the LinkedList class (the wrapper). When the wrapper invokes self.head.print_backward, it is invoking the helper, because self.head is a Node object.

Another benefit of the LinkedList class is that it makes it easier to add or remove the first element of a list. For example, add_first is a method for LinkedLists; it takes an item of cargo as an argument and puts it at the beginning of the list:

class LinkedList:
    ...
    def add_first(self, cargo):
        node = Node(cargo)
        node.next = self.head
        self.head = node
        self.length += 1

As usual, you should check code like this to see if it handles the special cases. For example, what happens if the list is initially empty?

24.10. Invariants

Some lists are well formed; others are not. For example, if a list contains a loop, it will cause many of our methods to crash, so we might want to require that lists contain no loops. Another requirement is that the length value in the LinkedList object should be equal to the actual number of nodes in the list.

Requirements like these are called invariants because, ideally, they should be true of every object all the time. Specifying invariants for objects is a useful programming practice because it makes it easier to prove the correctness of code, check the integrity of data structures, and detect errors.

One thing that is sometimes confusing about invariants is that there are times when they are violated. For example, in the middle of add_first, after we have added the node but before we have incremented length, the invariant is violated. This kind of violation is acceptable; in fact, it is often impossible to modify an object without violating an invariant for at least a little while. Normally, we require that every method that violates an invariant must restore the invariant.

If there is any significant stretch of code in which the invariant is violated, it is important for the comments to make that clear, so that no operations are performed that depend on the invariant.

24.11. Glossary

embedded reference

A reference stored in an attribute of an object.

linked list

A data structure that implements a collection using a sequence of linked nodes.

node

An element of a list, usually implemented as an object that contains a reference to another object of the same type.

cargo

An item of data contained in a node.

link

An embedded reference used to link one object to another.

precondition

An assertion that must be true in order for a method to work correctly.

fundamental ambiguity theorem

A reference to a list node can be treated as a single object or as the first in a list of nodes.

singleton

A linked list with a single node.

wrapper

A method that acts as a middleman between a caller and a helper method, often making the method easier or less error-prone to invoke.

helper

A method that is not invoked directly by a caller but is used by another method to perform part of an operation.

invariant

An assertion that should be true of an object at all times (except perhaps while the object is being modified).

24.12. Exercises

1. By convention, lists are often printed in brackets with commas between the elements, as in [1, 2, 3]. Modify print_list so that it generates output in this format.