6. Iteration

Computers are often used to automate repetitive tasks. Repeating identical or similar tasks without making errors is something that computers do well and people do poorly.

Repeated execution of a set of statements is called iteration. Because iteration is so common, Python provides several language features to make it easier. We’ve already been using the for statement since chapter 3. This is the form of iteration you’ll likely be using most often.

In this chapter we’re going to look at the while statement — another way to have your program do iteration, useful in somewhat different circumstances.

Before we do that, let’s just review a few ideas...

6.1. Reassignment

As we have mentioned previously, it is legal to make more than one assignment to the same variable. A new assignment makes an existing variable refer to a new value (and stop referring to the old value).

bruce = 5
print(bruce)
bruce = 7
print(bruce)

The output of this program is:

5
7

because the first time bruce is printed, its value is 5, and the second time, its value is 7.

Here is what reassignment looks like in a state snapshot:

With reassignment it is especially important to distinguish between an assignment statement and a boolean expression that tests for equality. Because Python uses the equal token (=) for assignment, it is tempting to interpret a statement like a = b as a boolean test. Unlike mathematics, it is not! Remember that the Python token for the equality operator is ==.

Note too that an equality test is symmetric, but assignment is not. For example, if a == 7 then 7 == a. But in Python, the statement a = 7 is legal and 7 = a is not.

Furthermore, in mathematics, a statement of equality is always true. If a == b now, then a will always equal b. In Python, an assignment statement can make two variables equal, but because of the possibility of reassignment, they don’t have to stay that way:

a = 5
b = a    # after executing this line, a and b are now equal
a = 3    # after executing this line, a and b are no longer equal

The third line changes the value of a but does not change the value of b, so they are no longer equal. (In some programming languages, a different symbol is used for assignment, such as <- or :=, to avoid confusion. Python chose to use the tokens = for assignment, and == for equality. This is a popular choice also found in languages like C, C++, Java, and C#.)

6.2. Updating variables

One of the most common forms of reassignment is an update, where the new value of the variable depends on the old.

x = x + 1

This means get the current value of x, add one, and then update x with the new value.

If you try to update a variable that doesn’t exist, you get an error, because Python evaluates the expression on the right side of the assignment operator before it assigns the resulting value to the name on the left:

>>> x = x + 1
Traceback (most recent call last):
  File "<interactive input>", line 1, in
NameError: name 'x' is not defined

Before you can update a variable, you have to initialize it, usually with a simple assignment:

>>> x = 0
>>> x = x + 1
>>>

Updating a variable by adding 1 is called an increment; subtracting 1 is called a decrement. Sometimes programmers also talk about bumping a variable, which means the same as incrementing it by 1.

6.3. The for loop revisited

Recall that the for loop processes each item in a list. Each item in turn is (re-)assigned to the loop variable, and the body of the loop is executed. We saw this example in an earlier chapter:

for f in ["Joe", "Amy", "Brad", "Angelina", "Zuki", "Thandi", "Paris"]:
    invitation = "Hi " + f + ".  Please come to my party on Saturday!"
    print(invitation)

Running through all the items in a list is called traversing the list, or traversal.

Let us write a function now to sum up all the elements in a list of numbers. Do this by hand first, and try to isolate exactly what steps you take. You’ll find you need to keep some “running total” of the sum so far, either on a piece of paper, or in your head. Remembering things from one step to the next is precisely why we have variables in a program: so we’ll need some variable to remember the “running total”. It should be initialized with a value of zero, and then we need to traverse the items in the list. For each item, we’ll want to update the running total by adding the next number to it.

def mysum(xs):
    """ Sum all the numbers in the list xs, and return the total. """
    running_total = 0
    for x in xs:
        running_total = running_total + x
    return running_total

#add tests like these to your test suite ...
test(mysum([1, 2, 3, 4]), 10)
test(mysum([1.25, 2.5, 1.75]), 5.5)
test(mysum([1, -2, 3]), 2)
test(mysum([ ]), 0)
test(mysum(range(11)), 55)    # Remember that 11 is not in the list that range generates.

6.4. The while statement

Here is a fragment of code that demonstrates the use of the while statement:

def sum_to(n):
    """ Return the sum of 1+2+3 ... n """
    ss  = 0
    v = 1
    while v <= n:
        ss = ss + v
        v = v + 1
    return ss

# for your test suite
test(sum_to(4), 10)
test(sum_to(1000), 500500)

You can almost read the while statement as if it were English. It means, While v is less than or equal to n, continue executing the body of the loop. Within the body, each time, increment v. When v passes n, return your accumulated sum.

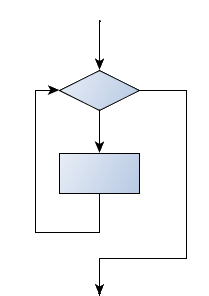
More formally, here is the flow of execution for a while statement:

1. Evaluate the condition, yielding False or True.
2. If the condition is false, exit the while statement and continue execution at the next statement.
3. If the condition is true, execute each of the statements in the body and then go back to step 1.

The body consists of all of the statements below the header with the same indentation.

This type of flow is called a loop because the third step loops back around to the top. Notice that if the condition is false the first time through the loop, the statements inside the loop are never executed.

The body of the loop should change the value of one or more variables so that eventually the condition becomes false and the loop terminates. Otherwise the loop will repeat forever, which is called an infinite loop. An endless source of amusement for computer scientists is the observation that the directions on shampoo, lather, rinse, repeat, are an infinite loop.

In the case here, we can prove that the loop terminates because we know that the value of n is finite, and we can see that the value of v increments each time through the loop, so eventually it will have to exceed n. In other cases, it is not so easy to tell.

What you will notice here is that the while loop is more work for you — the programmer — than the equivalent for loop. When using a while loop one has to control the loop variable yourself: give it an initial value, test for completion, and then make sure you change something in the body so that the loop terminates. By comparison, here is an alternative function that uses for instead:

def sum_to(n):
    """ Return the sum of 1+2+3 ... n """
    ss  = 0
    for v in range(n+1):
        ss = ss + v
    return ss

Notice the slightly tricky call to the range function — we had to add one onto n, because range generates its list up to but not including the value you give it. It would be easy to make a programming mistake and overlook this, but because we’ve made the investment of writing some unit tests, our test suite would have caught our error.

So why have two kinds of loop if for looks easier? This next example shows a case where we need the extra power that we get from the while loop.

6.5. The 3n + 1 sequence

Let’s look at a simple sequence that has fascinated and foxed mathematicians for many years. They still cannot answer even quite simple questions about this.

The rule is to atart from some given n, and to generate the next term of the sequence from n, either by halving n, (whenever n is even), or else by multiplying it by three and adding 1. The sequence terminates when n reaches 1.

This Python function captures that algorithm:

def seq3np1(n):
    """ Print the 3n+1 sequence from n, terminating when it reaches 1."""
    while n != 1:
        print(n, end=', ')
        if n % 2 == 0:        # n is even
            n = n // 2
        else:                 # n is odd
            n = n * 3 + 1
    print(n, end='.\n')

Notice first that the print function has an extra argument end=', '. This tells the print function to follow the printed string with whatever the programmer chooses (in this case, a comma followed by a space), instead of ending the line. So each time something is printed in the loop, it is printed on the same line, with the output separated by commas. The call to print(n, end='.\n') when the loop terminates will then print the final value of n followed by a period and a newline character. (You’ll cover the \n (newline character) in the next chapter).

The condition for this loop is n != 1, so the loop will continue running until n is 1, which will make the condition false.

Each time through the loop, the program outputs the value of n and then checks whether it is even or odd. If it is even, the value of n is divided by 2 using integer division. If it is odd, the value is replaced by n * 3 + 1.

Here are some examples:

>>> seq3np1(3)
3, 10, 5, 16, 8, 4, 2, 1.
>>> seq3np1(19)
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
>>> seq3np1(21)
21, 64, 32, 16, 8, 4, 2, 1.
>>> seq3np1(16)
16, 8, 4, 2, 1.
>>>

Since n sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the program terminates. For some particular values of n, we can prove termination. For example, if the starting value is a power of two, then the value of n will be even each time through the loop until it reaches 1. The previous example ends with such a sequence, starting with 16.

You might like to have some fun and see if you can find a small starting number that needs more than a hundred steps before it terminates.

Particular values aside, the interesting question is whether we can prove that this sequence terminates for all values of n. So far, no one has been able to prove it or disprove it!

Think carefully about what would be needed for a proof or disproof of the hypothesis “All positive integers will eventually converge to 1”. With fast computers we have been able to test every integer up to very large values, and so far, they all eventually end up at 1. But this doesn’t mean that there might not be some as-yet untested number which does not reduce to 1.

You’ll notice that if you don’t stop when you reach one the sequence gets into its own loop: 1, 4, 2, 1, 4, 2, 1, 4 ... So one possibility is that there might be other cycles that we just haven’t found.

Choosing between for and while

Use a for loop if you know the maximum number of times that you’ll need to execute the body. For example, if you’re traversing a list of elements, or can formulate a suitable call to range, then choose the for loop.

So any problem like “iterate this weather model run for 1000 cycles”, or “search this list of words”, “find all prime numbers up to 10000” suggest that a for loop is best.

By contrast, if you are required to repeat some computation until some condition is met, as we did in this 3n + 1 problem, you’ll need a while loop.

We call the first case definite iteration — we have some definite bounds for what is needed. The latter case is called indefinite iteration — we’re not sure how many iterations we’ll need — we cannot even establish an upper bound!

6.6. Tracing a program

To write effective computer programs a programmer needs to develop the ability to trace the execution of a computer program. Tracing involves becoming the computer and following the flow of execution through a sample program run, recording the state of all variables and any output the program generates after each instruction is executed.

To understand this process, let’s trace the call to seq3np1(3) from the previous section. At the start of the trace, we have a local variable, n (the parameter), with an initial value of 3. Since 3 is not equal to 1, the while loop body is executed. 3 is printed and 3 % 2 == 0 is evaluated. Since it evaluates to False, the else branch is executed and 3 * 3 + 1 is evaluated and assigned to n.

To keep track of all this as you hand trace a program, make a column heading on a piece of paper for each variable created as the program runs and another one for output. Our trace so far would look something like this:

n               output printed so far
--              ---------------------
3               3,
10

Since 10 != 1 evaluates to True, the loop body is again executed, and 10 is printed. 10 % 2 == 0 is true, so the if branch is executed and n becomes 5. By the end of the trace we have:

n               output printed so far
--              ---------------------
3               3,
10              3, 10,
5               3, 10, 5,
16              3, 10, 5, 16,
8               3, 10, 5, 16, 8,
4               3, 10, 5, 16, 8, 4,
2               3, 10, 5, 16, 8, 4, 2,
1               3, 10, 5, 16, 8, 4, 2, 1.

Tracing can be a bit tedious and error prone (that’s why we get computers to do this stuff in the first place!), but it is an essential skill for a programmer to have. From this trace we can learn a lot about the way our code works. We can observe that as soon as n becomes a power of 2, for example, the program will require log₂(n) executions of the loop body to complete. We can also see that the final 1 will not be printed as output within the body of the loop, which is why we put the special print function at the end.

Tracing a program is, of course, related to single-stepping through your code and being able to inspect the variables. Using the computer to single-step for you is less error prone and more convenient. Also, as your ptograms get more complex, they might execute many millions of steps before they get to the code that you’re really interested in, so manual tracing becomes impossible. Being able to set a breakpoint where you need one is far more powerful. So we strongly encourage you to invest time in learning using to use your programming environment (PyScripter, in these notes) to full effect.

We’ve cautioned against chatterbox functions, but used them here. As we learn a bit more Python, we’ll be able to show you how to generate a list of values to hold the sequence, rather than having the function print them. Doing this would remove the need to have all these pesky print functions in the middle of our logic, and will make the function more useful.

6.7. Counting digits

The following function counts the number of decimal digits in a positive integer:

def num_digits(n):
    count = 0
    while n > 0:
        count = count + 1
        n = n // 10
    return count

A call to print(num_digits(710)) will display 3. Trace the execution of this function call (perhaps using the single step function in PyScripter, or the Python visualizer, or on some paper) to convince yourself that it works.

This function demonstrates an important pattern of computation called a counter. The variable count is initialized to 0 and then incremented each time the loop body is executed. When the loop exits, count contains the result — the total number of times the loop body was executed, which is the same as the number of digits.

If we wanted to only count digits that are either 0 or 5, adding a conditional before incrementing the counter will do the trick:

def num_zero_and_five_digits(n):
    count = 0
    while n > 0:
        digit = n % 10
        if digit == 0 or digit == 5:
            count = count + 1
        n = n // 10
    return count

Confirm that test(num_zero_and_five_digits(1055030250), 7) passes.

Notice, however, that some of the tests below fail. Explain why. Do you think this is a bug in the code, or a bug in the specifications, our expectations, or the tests?

test(num_digits(1055030250), 10)
test(num_digits(0050), 4)
test(num_digits(0), 1)

6.8. Abbreviated assignment

Incrementing a variable is so common that Python provides an abbreviated syntax for it:

>>> count = 0
>>> count += 1
>>> count
1
>>> count += 1
>>> count
2
>>>

count += 1 is an abreviation for count = count + 1 . We pronouce the operator as “plus-equals”. The increment value does not have to be 1:

>>> n = 2
>>> n += 5
>>> n
7
>>>

There are similar abbreviations for -=, *=, /=, //= and %=:

>>> n = 2
>>> n \*= 5
>>> n
10
>>> n -= 4
>>> n
6
>>> n //= 2
>>> n
3
>>> n %= 2
>>> n
1

6.9. Tables

One of the things loops are good for is generating tabular data. Before computers were readily available, people had to calculate logarithms, sines and cosines, and other mathematical functions by hand. To make that easier, mathematics books contained long tables listing the values of these functions. Creating the tables was slow and boring, and they tended to be full of errors.

When computers appeared on the scene, one of the initial reactions was, “This is great! We can use the computers to generate the tables, so there will be no errors.” That turned out to be true (mostly) but shortsighted. Soon thereafter, computers and calculators were so pervasive that the tables became obsolete.

Well, almost. For some operations, computers use tables of values to get an approximate answer and then perform computations to improve the approximation. In some cases, there have been errors in the underlying tables, most famously in the table the Intel Pentium processor chip used to perform floating-point division.

Although a log table is not as useful as it once was, it still makes a good example of iteration. The following program outputs a sequence of values in the left column and 2 raised to the power of that value in the right column:

for x in range(13):   # generate numbers 0 to 12
    print(x, '\t', 2**x)

The string '\t' represents a tab character. The backslash character in '\t' indicates the beginning of an escape sequence. Escape sequences are used to represent invisible characters like tabs and newlines. The sequence \n represents a newline.

An escape sequence can appear anywhere in a string; in this example, the tab escape sequence is the only thing in the string. How do you think you represent a backslash in a string?

As characters and strings are displayed on the screen, an invisible marker called the cursor keeps track of where the next character will go. After a print function, the cursor normally goes to the beginning of the next line.

The tab character shifts the cursor to the right until it reaches one of the tab stops. Tabs are useful for making columns of text line up, as in the output of the previous program:

0       1
1       2
2       4
3       8
4       16
5       32
6       64
7       128
8       256
9       512
10      1024
11      2048
12      4096

Because of the tab characters between the columns, the position of the second column does not depend on the number of digits in the first column.

6.10. Two-dimensional tables

A two-dimensional table is a table where you read the value at the intersection of a row and a column. A multiplication table is a good example. Let’s say you want to print a multiplication table for the values from 1 to 6.

A good way to start is to write a loop that prints the multiples of 2, all on one line:

for i in range(1, 7):
    print(2 * i, end='   ')
print()

Here we’ve used the range function, but made it start its sequence at 1. As the loop executes, the value of i changes from 1 to 6. When all the elements of the range have been assigned to i, the loop terminates. Each time through the loop, it displays the value of 2 * i, followed by three spaces.

Again, the extra end='   ' argument in the print function suppresses the newline, and uses three spaces instead. After the loop completes, the second call to print finishes the current line, and starts a new line.

The output of the program is:

2      4      6      8      10     12

So far, so good. The next step is to encapsulate and generalize.

6.11. Encapsulation and generalization

Encapsulation is the process of wrapping a piece of code in a function, allowing you to take advantage of all the things functions are good for. You have already seen some examples of encapsulation, including is_divisible in a previous chapter.

Generalization means taking something specific, such as printing the multiples of 2, and making it more general, such as printing the multiples of any integer.

This function encapsulates the previous loop and generalizes it to print multiples of n:

def print_multiples(n):
    for i in range(1, 7):
        print(n * i, end='   ')
    print()

To encapsulate, all we had to do was add the first line, which declares the name of the function and the parameter list. To generalize, all we had to do was replace the value 2 with the parameter n.

If we call this function with the argument 2, we get the same output as before. With the argument 3, the output is:

3      6      9      12     15     18

With the argument 4, the output is:

4      8      12     16     20     24

By now you can probably guess how to print a multiplication table — by calling print_multiples repeatedly with different arguments. In fact, we can use another loop:

for i in range(1, 7):
    print_multiples(i)

Notice how similar this loop is to the one inside print_multiples. All we did was replace the print function with a function call.

The output of this program is a multiplication table:

1      2      3      4      5      6
2      4      6      8      10     12
3      6      9      12     15     18
4      8      12     16     20     24
5      10     15     20     25     30
6      12     18     24     30     36

6.12. More encapsulation

To demonstrate encapsulation again, let’s take the code from the last section and wrap it up in a function:

def print_mult_table():
    for i in range(1, 7):
        print_multiples(i)

This process is a common development plan. We develop code by writing lines of code outside any function, or typing them in to the interpreter. When we get the code working, we extract it and wrap it up in a function.

This development plan is particularly useful if you don’t know how to divide the program into functions when you start writing. This approach lets you design as you go along.

6.13. Local variables

You might be wondering how we can use the same variable, i, in both print_multiples and print_mult_table. Doesn’t it cause problems when one of the functions changes the value of the variable?

The answer is no, because the i in print_multiples and the i in print_mult_table are not the same variable.

Variables created inside a function definition are local; you can’t access a local variable from outside its home function. That means you are free to have multiple variables with the same name as long as they are not in the same function.

The stack diagram for this program shows that the two variables named i are not the same variable. They can refer to different values, and changing one does not affect the other.

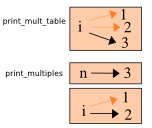
The value of i in print_mult_table goes from 1 to 6. In the diagram it happens to be 3. The next time through the loop it will be 4. Each time through the loop, print_mult_table calls print_multiples with the current value of i as an argument. That value gets assigned to the parameter n.

Inside print_multiples, the value of i goes from 1 to 6. In the diagram, it happens to be 2. Changing this variable has no effect on the value of i in print_mult_table.

It is common and perfectly legal to have different local variables with the same name. In particular, names like i and j are used frequently as loop variables. If you avoid using them in one function just because you used them somewhere else, you will probably make the program harder to read.

6.14. The break statement, and flavours of loops

A pre-test loop

The break statement is used to immediately leave the body of its loop. The next statement to be executed is the first one after the body:

for i in [12, 16, 17, 24, 29]:
    if i % 2 == 1:  # if the number is odd
       break        # immediately exit the loop
    print(i)
print("done")

This prints:

12
16
done

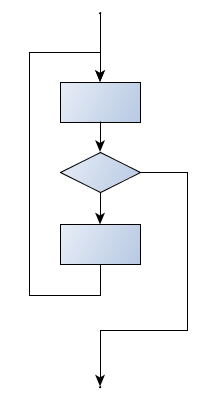
for and while loops do their tests at the start, before executing any part of the body. (They’re called pre-test loops, because the test happens before (pre) the body.)

A middle-test loop

Sometimes we’d like to have the middle-test loop with the exit test in the middle of the body, rather than at the beginning. Or a post-test loop that puts its exit test after the body. Python doesn’t provide different loops for these cases: but a combination of while and break are sufficient to get the job done.

A typical example is a problem where the user has to input numbers to be summed. To indicate that there are no more inputs, the user enters a special value, often the value -1, or the empty string. This needs a middle-exit loop pattern: input the next number, then test whether to exit, or else process the number:

total = 0
while True:
    response = input("Enter the next number. (Leave blank to end)")
    if response == "":
        break
    total += int(response)
print("The total of the numbers you entered is ", total)

A post-test loop would be useful,for example, if you were playing an interactive game against the user:

while True:
    play_the_game()
    response = input("Play again? (yes or no)")
    if response != "yes":
        break
print("Goodbye!")

A post-test loop

The while True: in these cases is idiomatic — a convention that most programmers will recognize immediately. The test in the while loop must always succeed. A clever compiler or interpreter will understand that and won’t generate any unnecessary work!

The following program implements a simple guessing game:

import random

number = random.randint(1, 1000)
guesses = 0

print("I'm thinking of a number between 1 and 1000.")

while True:
    guess = int(input("\nWhat do you think it is? "))
    guesses += 1

    if guess > number:
        print("{0} is too high.".format(guess))
    elif guess < number: 
        print("{0} is too low.".format(guess))
    else:
        break

print("\nCongratulations, you got it in {0} guesses!\n".format(guesses))

This program makes use of the mathematical law of trichotomy (given real numbers a and b, exactly one of these three must be true: a > b, a < b, or a == b).

6.15. The continue statement

This is a control flow statement that causes the program to immediately skip the processing of the rest of the body of the loop, for the current iteration. But the loop still carries on running for its remaining iterations:

for i in [12, 16, 17, 24, 29, 30]:
    if i % 2 == 1:      # if the number is odd
       continue         # don't process it
    print(i)
print("done")

This prints:

12
16
24
30
done

6.16. More generalization

As another example of generalization, imagine you wanted a program that would print a multiplication table of any size, not just the six-by-six table. You could add a parameter to print_mult_table:

def print_mult_table(high):
    for i in range(1, high+1):
        print_multiples(i)

We replaced the value 1 with the expression high+1. If we call print_mult_table with the argument 7, it displays:

1      2      3      4      5      6
2      4      6      8      10     12
3      6      9      12     15     18
4      8      12     16     20     24
5      10     15     20     25     30
6      12     18     24     30     36
7      14     21     28     35     42

This is fine, except that we probably want the table to be square — with the same number of rows and columns. To do that, we add another parameter to print_multiples to specify how many columns the table should have.

Just to be annoying, we call this parameter high, demonstrating that different functions can have parameters with the same name (just like local variables). Here’s the whole program:

def print_multiples(n, high):
    for i in range(1, high+1):
        print(n * i, end='   ')
    print()

def print_mult_table(high):
    for i in range(1, high+1):
        print_multiples(i, high)

Notice that when we added a new parameter, we had to change the first line of the function (the function heading), and we also had to change the place where the function is called in print_mult_table.

Now, when we call print_mult_table(7):

1      2      3      4      5      6      7
2      4      6      8      10     12     14
3      6      9      12     15     18     21
4      8      12     16     20     24     28
5      10     15     20     25     30     35
6      12     18     24     30     36     42
7      14     21     28     35     42     49

When you generalize a function appropriately, you often get a program with capabilities you didn’t plan. For example, you might notice that, because ab = ba, all the entries in the table appear twice. You could save ink by printing only half the table. To do that, you only have to change one line of print_mult_table. Change

print_multiples(i, high+1)

to

print_multiples(i, i+1)

and you get:

1
2      4
3      6      9
4      8      12     16
5      10     15     20     25
6      12     18     24     30     36
7      14     21     28     35     42     49

6.17. Functions

A few times now, we have mentioned all the things functions are good for. By now, you might be wondering what exactly those things are. Here are some of them:

1. Giving a name to a sequence of statements makes your program easier to read and debug.
2. Dividing a long program into functions allows you to separate parts of the program, debug them in isolation, and then compose them into a whole.
3. Functions facilitate the use of iteration.
4. Well-designed functions are often useful for many programs. Once you write and debug one, you can reuse it.

6.18. Newton’s Method

Loops are often used in programs that compute numerical results by starting with an approximate answer and iteratively improving it.

For example, one way of computing square roots is Newton’s method. Suppose that you want to know the square root of n. If you start with almost any approximation, you can compute a better approximation with the following formula:

better =  (approx + n/approx)/2

Execute this algorithm a few times using your calculator. Can you see why each iteration brings your estimate a little closer? One of the amazing properties of this particular algorithm is how quickly it converges to an accurate answer.

By repeatedly applying this formula until the better approximation gets close enough to the previous one, we can write a function for computing the square root.

def sqrt(n):
    approx = n/2.0
    better = (approx + n/approx)/2.0
    while  better !=  approx):
        approx = better
        better = (approx + n/approx)/2.0
    return approx

# test cases
test(sqrt(25.0), 5.0)
test(sqrt(49.0), 7.0)
test(sqrt(81.0), 9.0)

6.19. Algorithms

Newton’s method is an example of an algorithm: it is a mechanical process for solving a category of problems (in this case, computing square roots).

It is not easy to define an algorithm. It might help to start with something that is not an algorithm. When you learned to multiply single-digit numbers, you probably memorized the multiplication table. In effect, you memorized 100 specific solutions. That kind of knowledge is not algorithmic.

But if you were lazy, you probably cheated by learning a few tricks. For example, to find the product of n and 9, you can write n - 1 as the first digit and 10 - n as the second digit. This trick is a general solution for multiplying any single-digit number by 9. That’s an algorithm!

Similarly, the techniques you learned for addition with carrying, subtraction with borrowing, and long division are all algorithms. One of the characteristics of algorithms is that they do not require any intelligence to carry out. They are mechanical processes in which each step follows from the last according to a simple set of rules.

In our opinion, it is embarrassing that humans spend so much time in school learning to execute algorithms that, quite literally, require no intelligence.

On the other hand, understanding that hard problems can be solved by step-by-step algorithmic processess is one of the major simplifying breakthroughs that has had enormous benefits. So while the execution of the algorithm may be boring and may require no intelligence, algorithmic or computational thinking is having a vast impact. And the process of designing algorithms is interesting, intellectually challenging, and a central part of what we call programming.

Some of the things that people do naturally, without difficulty or conscious thought, are the hardest to express algorithmically. Understanding natural language is a good example. We all do it, but so far no one has been able to explain how we do it, at least not in the form of a step-by-step mechanical algorithm.

6.20. Glossary

algorithm

A step-by-step process for solving a category of problems.

body

The statements inside a loop.

breakpoint

A place in your program code where program execution will pause (or break), allowing you to inspect the state of the program’s variables, or single-step through individual statements, executing them one at a time.

bump

Programmer slang. Synonym for increment.

counter

A variable used to count something, usually initialized to zero and incremented in the body of a loop.

cursor

An invisible marker that keeps track of where the next character will be printed.

decrement

Decrease by 1.

definite iteration

A loop where we have an upper bound on the number of times the body will be executed. Definite iteration is usually best coded as a for loop.

development plan

A process for developing a program. In this chapter, we demonstrated a style of development based on developing code to do simple, specific things and then encapsulating and generalizing.

encapsulate

To divide a large complex program into components (like functions) and isolate the components from each other (by using local variables, for example).

escape sequence

An escape character, \, followed by one or more printable characters used to designate a nonprintable character.

generalize

To replace something unnecessarily specific (like a constant value) with something appropriately general (like a variable or parameter). Generalization makes code more versatile, more likely to be reused, and sometimes even easier to write.

increment

Both as a noun and as a verb, increment means to increase by 1.

infinite loop

A loop in which the terminating condition is never satisfied.

indefinite iteration

A loop where we just need to keep going until some condition is met. A while statement is used for this case.

initialization (of a variable)

To initialize a variable is to give it an initial value. Since in Python variables don’t exist until they are assigned values, they are initialized when they are created. In other programming languages this is not the case, and variables can be created without being initialized, in which case they have either default or garbage values.

iteration

Repeated execution of a set of programming statements.

loop

A statement or group of statements that execute repeatedly until a terminating condition is satisfied.

loop variable

A variable used as part of the terminating condition of a loop.

meta-notation

Extra symbols or notation that helps describe other notation. Here we introduced square brackets, ellipses, italics, and bold as meta-notation to help describe optional, repeatable, substitutable and fixed parts of the Python syntax.

middle-test loop

A loop that executes some of the body, then tests for the exit condition, and then may execute some more of the body. We don’t have a special Python construct for this case, but can use while and break together.

nested loop

A loop inside the body of another loop.

newline

A special character that causes the cursor to move to the beginning of the next line.

post-test loop

A loop that executes the body, then tests for the exit condition. We don’t have a special Python construct for this, but can use while and break together.

pre-test loop

A loop that tests before deciding whether the execute its body. for and while are both pre-test loops.

reassignment

Making more than one assignment to the same variable during the execution of a program.

single-step

A mode of interpreter execution where you are able to execute your program one step at a time, and inspect the consequences of that step. Useful for debugging and building your internal mental model of what is going on.

tab

A special character that causes the cursor to move to the next tab stop on the current line.

trichotomy

Given any real numbers a and b, exactly one of the following relations holds: a < b, a > b, or a == b. Thus when you can establish that two of the relations are false, you can assume the remaining one is true.

trace

To follow the flow of execution of a program by hand, recording the change of state of the variables and any output produced.

6.21. Exercises

This chapter showed us how to sum a list of items, and how to count items. The counting example also had an if statement that let us only count some selected items. In the previous chapter we also showed a function find_first_2_letter_word that allowed us an “early exit” from inside a loop by using return when some condition occurred. We now also have break to exit a loop (but not the enclosing function, and continue to abandon the current iteration of the loop without ending the loop.

Composition of list traversal, summing, counting, testing conditions and early exit is a rich collection of building blocks that can be combined in powerful ways to create many functions that are all slightly different.

The first six questions are typical functions you should be able to write using only these building blocks.

1. Write a function to count how many odd numbers are in a list.

2. Sum up all the even numbers in a list.

3. Sum up all the negative numbers in a list.

4. Count how many words in a list have length 5.

5. Sum all the elements in a list up to but not including the first even number. (Write your unit tests. What if there is no even number?)

6. Count how many words occur in a list up to and including the first occurrence of the word “sam”. (Write your unit tests for this case too. What if “sam” does not occur?)

7. Add a print function to Newton’s sqrt function that prints out better each time it is calculated. Call your modified function with 25 as an argument and record the results.

8. Trace the execution of the last version of print_mult_table and figure out how it works.

9. Write a function print_triangular_numbers(n) that prints out the first n triangular numbers. A call to print_triangular_numbers(5) would produce the following output:

   1       1
   2       3
   3       6
   4       10
   5       15

   (hint: use a web search to find out what a triangular number is.)

10. Write a function, is_prime, which takes a single integer argument and returns True when the argument is a prime number and False otherwise. Add tests for cases like this:

    test(is_prime(11), True)
    test(is_prime(35), False)
    test(is_prime(19911129), True)
    

    The last case could represent your birth date. Were you born on a prime day? In a class of 100 students, how many do you think would have prime birth dates?

11. Revisit the drunk student problem from the exercises in chapter 3. Now write a function that gets the student to make 50 random turns and moves. Each random turn should be an angle between 0 and 360, and each move should be a random move forward between 0 and 100 steps. Use the turtle module to plot these. Peek ahead to the section on random numbers (look it up in the index) to see how to make the computer generate random numbers for you.

12. What will num_digits(0) return? Modify it to return 1 for this case. Why does a call to num_digits(-24) result in an infinite loop? (hint: -1//10 evaluates to -1) Modify num_digits so that it works correctly with any integer value. Add these tests:

    test(num_digits(0), 1)
    test(num_digits(-12345), 5)
    

13. Write a function num_even_digits(n) that counts the number of even digits in n. These tests should pass:

    test(num_even_digits(123456), 3)
    test(num_even_digits(2468), 4)
    test(num_even_digits(1357), 0)
    test(num_even_digits(0), 1)
    

14. Write a function sum_of_squares(xs) that computes the sum of the squares of the numbers in the list xs. For example, sum_of_squares([2, 3, 4]) should return 4+9+16 which is 29:

    test(sum_of_squares([2, 3, 4]), 29)
    test(sum_of_squares([ ]), 0)
    test(sum_of_squares([2, -3, 4]), 29)
    

15. You and your friend are in a team to write a two-player game, human against computer, such as Tic-Tac-Toe / Noughts and Crosses. Your friend will write the logic to play one round of the game, while you will write the logic to allow many rounds of play, keep score, decide who plays, first, etc. The two of you negotiate on how the two parts of the program will interact with each other, and you come up with this simple scaffolding (which your friend will improve later):

    def play_once(human_plays_first):
        """
           Must play one round of the game. If the parameter is True, the
           human gets to play first, else the computer gets to play first.
           When the round ends, the return value of the function is one of
           -1 (human wins),  0 (game drawn),   1 (computer wins).
        """
        # This is all dummy code right at the moment...
        import random                # see ch 10 for details
        rng = random.Random()
        result = rnd.randrange(-1,2) # pick a random result.
        print("Human plays first={0},  winner={1} ".format(human_plays_first, result))
        return result
    

    1. Write the main program which repeatedly calls the function to play the game, and announces the outcome as “I win”. “You win”, or “Game drawn!”. It then asks the player “Do you want to play again?” and either plays again, or says “Goodbye”, and terminates.
    2. Keep score of how many wins each player has had, and how many draws there have been. After each round of play, announce the scores.
    3. Add logic to ensure that the player who gets to play first alternates on every round.
    4. Change the logic from part (c.) so that the player who won the previous round gets to play first.
    5. Compute the percentage of wins for the human, out of all games played. Announce this at the end of each round.
    6. Draw a flowchart of your logic.