





 |
 |
 |
 |
 |
 |
 |
The modulus operator works on integers (and integer expressions) and yields the remainder when the first operand is divided by the second. In Java, the modulus operator is a percent sign, %. The syntax is exactly the same as for other operators:
int quotient = 7 / 3;The first operator, integer division, yields 2. The second operator yields 1. Thus, 7 divided by 3 is 2 with 1 left over.
The modulus operator turns out to be surprisingly useful. For example, you can check whether one number is divisible by another: if x % y is zero, then x is divisible by y.
Also, you can use the modulus operator to extract the rightmost digit or digits from a number. For example, x % 10 yields the rightmost digit of x (in base 10). Similarly x % 100 yields the last two digits.
In order to write useful programs, we almost always need the ability to check certain conditions and change the behavior of the program accordingly. Conditional statements give us this ability. The simplest form is the if statement:
if (x > 0) {The expression in parentheses is called the condition. If it is true, then the statements in brackets get executed. If the condition is not true, nothing happens.
The condition can contain any of the comparison operators, sometimes called relational operators:
x == y // x equals yAlthough these operations are probably familiar to you, the syntax Java uses is a little different from mathematical symbols like =, \neq and \le. A common error is to use a single = instead of a double ==. Remember that = is the assignment operator, and == is a comparison operator. Also, there is no such thing as =< or =>.
The two sides of a condition operator have to be the same type. You can only compare ints to ints and doubles to doubles. Unfortunately, at this point you can't compare Strings at all! There is a way to compare Strings, but we won't get to it for a couple of chapters.
A second form of conditional execution is alternative execution, in which there are two possibilities, and the condition determines which one gets executed. The syntax looks like:
if (x%2 == 0) {If the remainder when x is divided by 2 is zero, then we know that x is even, and this code prints a message to that effect. If the condition is false, the second set of statements is executed. Since the condition must be true or false, exactly one of the alternatives will be executed.
As an aside, if you think you might want to check the parity (evenness or oddness) of numbers often, you might want to "wrap" this code up in a method, as follows:
public static void printParity (int x) {Now you have a method named printParity that will print an appropriate message for any integer you care to provide. In main you would invoke this method as follows:
printParity (17);Always remember that when you invoke a method, you do not have to declare the types of the arguments you provide. Java can figure out what type they are. You should resist the temptation to write things like:
int number = 17;Sometimes you want to check for a number of related conditions and choose one of several actions. One way to do this is by chaining a series of ifs and elses:
if (x > 0) {These chains can be as long as you want, although they can be difficult to read if they get out of hand. One way to make them easier to read is to use standard indentation, as demonstrated in these examples. If you keep all the statements and squiggly-brackets lined up, you are less likely to make syntax errors and you can find them more quickly if you do.
In addition to chaining, you can also nest one conditional within another. We could have written the previous example as:
if (x == 0) {There is now an outer conditional that contains two branches. The first branch contains a simple print statement, but the second branch contains another conditional statement, which has two branches of its own. Fortunately, those two branches are both print statements, although they could have been conditional statements as well.
Notice again that indentation helps make the structure apparent, but nevertheless, nested conditionals get difficult to read very quickly. In general, it is a good idea to avoid them when you can.
On the other hand, this kind of nested structure is common, and we will see it again, so you better get used to it.
The return statement allows you to terminate the execution of a method before you reach the end. One reason to use it is if you detect an error condition:
public static void printLogarithm (double x) {This defines a method named printLogarithm that takes a double named x as a parameter. The first thing it does is check whether x is less than or equal to zero, in which case it prints an error message and then uses return to exit the method. The flow of execution immediately returns to the caller and the remaining lines of the method are not executed.
I used a floating-point value on the right side of the condition because there is a floating-point variable on the left.
You might wonder how you can get away with an expression like "The log of x is " + result, since one of the operands is a String and the other is a double. Well, in this case Java is being smart on our behalf, by automatically converting the double to a String before it does the string concatenation.
This kind of feature is an example of a common problem in designing a programming language, which is that there is a conflict between formalism, which is the requirement that formal languages should have simple rules with few exceptions, and convenience, which is the requirement that programming languages be easy to use in practice.
More often than not, convenience wins, which is usually good for expert programmers (who are spared from rigorous but unwieldy formalism), but bad for beginning programmers, who are often baffled by the complexity of the rules and the number of exceptions. In this book I have tried to simplify things by emphasizing the rules and omitting many of the exceptions.
Nevertheless, it is handy to know that whenever you try to "add" two expressions, if one of them is a String, then Java will convert the other to a String and then perform string concatenation. What do you think happens if you perform an operation between an integer and a floating-point value?
In order to draw things on the screen, you need two objects, a Slate and a Graphics object.
The methods that pertain to Graphics objects are defined in the built-in Graphics class. The methods that pertain to Slates are defined in the Slate class, which is shown in Appendix C.
The primary method in the Slate class is makeSlate, which does pretty much what you would expect. It creates a new window and returns a Slate object you can use to refer to the window later in the program. You can create more than one Slate in a single program.
Slate slate = Slate.makeSlate (500, 500);makeSlate takes two arguments, the width and height of the screen. Because it belongs to a different class, we have to specify the name of the class using "dot notation."
The return value gets assigned to a variable named slate. There is no conflict between the name of the class (with an upper-case "S") and the name of the variable (with a lower-case "s").
The next method we need is getGraphics, which takes a Slate object and creates a Graphics object that can draw on it. You can think of a Graphics object as a piece of chalk.
Graphics g = Slate.getGraphics (slate);Using the name g is conventional, but we could have called it anything.
In order to draw things on the screen, you invoke methods on the graphics object. We have invoked lots of methods already, but this is the first time we have "invoked a method on an object." The syntax is similar to invoking a method from another class:
g.setColor (Color.black);The name of the object comes before the dot; the name of the method comes after, followed by the arguments for that method. In this case, the method takes a single argument, which is a color.
setColor changes the current color, in this case to black. Everything that gets drawn will be black, until we use setColor again.
Color.black is a special value provided by the Color class, just as Math.PI is a special value provided by the Math class. Color, you will be happy to hear, provides a palette of other colors, including:
black blue cyan darkGray gray lightGrayTo draw on the Slate, we can invoke draw methods on the Graphics object. For example:
g.drawOval (x, y, width, height);drawOval takes four integers as arguments. These arguments specify a bounding box, which is the rectangle in which the oval will be drawn (as shown in the figure). The bounding box itself is not drawn; only the oval is. The bounding box is like a guideline. Bounding boxes are always oriented horizontally or vertically; they are never at a funny angle.
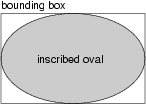
If you think about it, there are lots of ways to specify the location and size of a rectangle. You could give the location of the center or any of the corners, along with the height and width. Or, you could give the location of opposing corners. The choice is arbitrary, but in any case it will require the same number of parameters: four.
By convention, the usual way to specify a bounding box is to give the location of the upper-left corner and the width and height. The usual way to specify a location is to use a coordinate system.
You are probably familiar with Cartesian coordinates in two dimensions, in which each location is identified by an x-coordinate (distance along the x-axis) and a y-coordinate. By convention, Cartesian coordinates increase to the right and up, as shown in the figure.
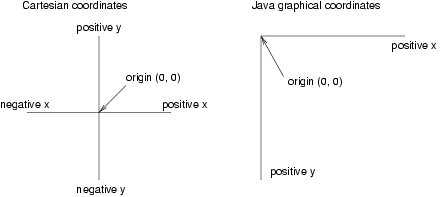
Annoyingly, it is conventional for computer graphics systems to use a variation on Cartesian coordinates in which the origin is in the upper-left corner of the screen or window, and the direction of the positive y-axis is down. Java follows this convention.
The unit of measure is called a pixel; a typical screen is about 1000 pixels wide. Coordinates are always integers. If you want to use a floating-point value as a coordinate, you have to round it off to an integer (See Section 3.2).
Let's say we want to draw a picture of Mickey Mouse. We can use the oval we just drew as the face, and then add ears. Before we do that it is a good idea to break the program up into two methods. main will create the Slate and Graphics objects and then invoke draw, which does the actual drawing.
public static void main (String[] args) {The parameters for draw are the Graphics object and a bounding box. draw invokes drawOval three times, to draw Mickey's face and two ears. The following figure shows the bounding boxes for the ears.
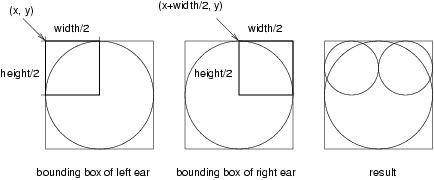
As shown in the figure, the coordinates of the upper-left corner of the bounding box for the left ear are (x, y). The coordinates for the right ear are (x+width/2, y). In both cases, the width and height of the ears are half the width and height of the original bounding box.
Notice that the coordinates of the ear boxes are all relative to the location (x and y) and size (width and height) of the original bounding box. As a result, we can use draw to draw a Mickey Mouse (albeit a lame one) anywhere on the screen in any size. As an exercise, modify the arguments passed to draw so that Mickey is one half the height and width of the screen, and centered.
Another drawing command with the same parameters as drawOval is
drawRect (int x, int y, int width, int height)Here I am using a standard format for documenting the name and parameters of methods. This information is sometimes called the method's interface or prototype. Looking at this prototype, you can tell what types the parameters are and (based on their names) infer what they do. Here's another example:
drawLine (int x1, int y1, int x2, int y2)The use of parameter names x1, x2, y1 and y2 suggests that drawLine draws a line from the point (x1, y1) to the point (x2, y2).
One other command you might want to try is
drawRoundRect (int x, int y, int width, int height,The first four parameters specify the bounding box of the rectangle; the remaining two parameters indicate how rounded the corners should be, specifying the horizontal and vertical diameter of the arcs at the corners.
There are also "fill" versions of these commands, that not only draw the outline of a shape, but also fill it in. The interfaces are identical; only the names have been changed:
fillOval (int x, int y, int width, int height)There is no such thing as fillLine---it just doesn't make sense.
I mentioned in the last chapter that it is legal for one method to call another, and we have seen several examples of that. I neglected to mention that it is also legal for a method to invoke itself. It may not be obvious why that is a good thing, but it turns out to be one of the most magical and interesting things a program can do.
For example, look at the following method:
public static void countdown (int n) {The name of the method is countdown and it takes a single integer as a parameter. If the parameter is zero, it prints the word "Blastoff." Otherwise, it prints the number and then invokes a method named countdown---itself---passing n-1 as an argument.
What happens if we invoke this method, in main, like this:
countdown (3);The execution of countdown begins with n=3, and since n is not zero, it prints the value 3, and then invokes itself...
The execution of countdown begins with n=2, and since n is not zero, it prints the value 2, and then invokes itself...
The execution of countdown begins with n=1, and since n is not zero, it prints the value 1, and then invokes itself...
The execution of countdown begins with n=0, and since n is zero, it prints the word "Blastoff!" and then returns.
The countdown that got n=1 returns.
The countdown that got n=2 returns.
The countdown that got n=3 returns.
And then you're back in main (what a trip). So the total output looks like:
3As a second example, let's look again at the methods newLine and threeLine.
public static void newLine () {Although these work, they would not be much help if I wanted to print 2 newlines, or 106. A better alternative would be
public static void nLines (int n) {This program is very similar; as long as n is greater than zero, it prints one newline, and then invokes itself to print n-1 additional newlines. Thus, the total number of newlines that get printed is 1 + (n-1), which usually comes out to roughly n.
The process of a method invoking itself is called recursion, and such methods are said to be recursive.
If you write recursive graphical methods, you often get interesting shapes called fractals. For example, to draw a fractal Mickey Mouse, we can modify draw so that it calls itself recursively:
public static void drawOnly a couple of changes are required. First, instead of invoking drawOval to draw the ears, we invoke draw to draw recursive ears; that is, ears that have ears that have ears of their own, and so on. Also, instead of invoking drawOval on the Graphics object g, we just invoke draw and pass g as an argument.
Finally, and most importantly, notice that I added a line at the beginning of the method that checks whether the height is equal to zero, and if it is, it returns immediately without drawing any circles, and without making any recursive calls. This is necessary because otherwise we would just draw smaller and smaller circles and the program would never terminate. This is known as infinite recursion, and it is generally not considered a good idea.
Actually, in Java an infinite recursion will eventually cause a StackOverflowException. If you ever get this error, you will know why.
The output of this program looks like this:
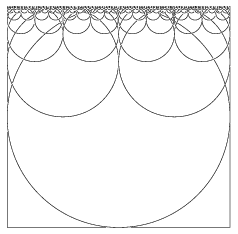
That might not seem too exciting yet, but with only a few modifications, you can get this:

Can you figure out how?
In the previous chapter we used a stack diagram to represent the state of a program during a method call. The same kind of diagram can make it easier to interpret a recursive method.
Remember that every time a method gets called it creates a new instance of the method that contains a new version of the method's local variables and parameters.
The following figure is a stack diagram for countdown, called with n = 3:
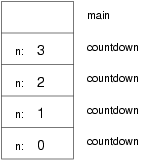
There is one instance of main and four instances of countdown, each with a different value for the parameter n. The bottom of the stack, countdown with n=0 is the base case. It does not make a recursive call, so there are no more instances of countdown.
The instance of main is empty because main does not have any parameters or local variables. As an exercise, draw a stack diagram for nLines, invoked with the parameter n=4.
In the last few sections, I used the phrase "by convention" several times to indicate design decisions that are arbitrary in the sense that there are no significant reasons to do things one way or another, but dictated by convention.
In these cases, it is to your advantage to be familiar with convention and use it, since it will make your programs easier for others to understand. At the same time, it is important to distinguish between (at least) three kinds of rules:
As we go along, I will try to indicate which category various things fall into, but you might want to give it some thought from time to time.
While I am on the topic, you have probably figured out by now that the names of classes always begin with a capital letter, but variables and methods begin with lower case. If a name includes more than one word, you usually capitalize the first letter of each word, as in newLine and printParity. Which category are these rules in?
 |
 |
 |
 |
 |
 |
 |