Chapter 10 Exercise Set 1¶

In the above description, the string "Point Kiukiu" still occurs three times in a row. We could make our description even more succinct by allowing multiple roads to be specified in one line.

Write a function makeRoads that takes any uneven number of arguments. The first argument is always the starting point of the roads, and every pair of arguments after that gives an ending point and a distance.

Do not duplicate the functionality of makeRoad, but have makeRoads call makeRoad to do the actual road-making.

function makeRoads(start) {
    for (var i = 1; i < arguments.length; i += 2)
        makeRoad(start, arguments[i], arguments[i + 1]);
}

This function uses one named parameter, start, and gets the other parameters from the arguments (quasi-) array. i starts at 1 because it has to skip this first parameter. i += 2 is short for i = i + 2, as you might recall.

var roads = {};
makeRoads("Point Kiukiu", "Hanaiapa", 19,
          "Mt Feani", 15, "Taaoa", 15);
makeRoads("Airport", "Hanaiapa", 6, "Mt Feani", 5,
          "Atuona", 4, "Mt Ootua", 11);
makeRoads("Mt Temetiu", "Mt Feani", 8, "Taaoa", 4);
makeRoads("Atuona", "Taaoa", 3, "Hanakee pearl lodge", 1);
makeRoads("Cemetery", "Hanakee pearl lodge", 6, "Mt Ootua", 5);
makeRoads("Hanapaoa", "Mt Ootua", 3);
makeRoads("Puamua", "Mt Ootua", 13, "Point Teohotepapapa", 14);

alert(roads["Airport"]);

Before starting to generate routes, we need one more higher-order function. This one is called filter. Like map, it takes a function and an array as arguments, and produces a new array, but instead of putting the results of calling the function in the new array, it produces an array with only those values from the old array for which the given function returns a true-like value. Write this function.
```
function filter(test, array) {
    var result = [];
    forEach(array, function (element) {
        if (test(element))
            result.push(element);
    });
    return result;
}

alert(filter(partial(op[">"], 5), [0, 4, 8, 12]));
```
(If the result of that application of filter surprises you, remember that the argument given to partial is used as the first argument of the function, so it ends up to the left of the >.)
Now that we have all possible routes, let us try to find the shortest one. Write a function shortestRoute that, like possibleRoutes, takes the names of a starting and ending location as arguments. It returns a single route object, of the type that possibleRoutes produces.
```
function shortestRoute(from, to) {
    var currentShortest = null;
    forEach(possibleRoutes(from, to), function(route) {
        if (!currentShortest || currentShortest.length > route.length)
            currentShortest = route;
    });
    return currentShortest;
}
```
The tricky thing in “minimising” or “maximising” algorithms is to not screw up when given an empty array. In this case, we happen to know that there is at least one road between every two places, so we could just ignore it. But that would be a bit lame. What if the road from Puamua to Mount Ootua, which is steep and muddy, is washed away by a rainstorm? It would be a shame if this caused our function to break as well, so it takes care to return null when no routes are found.

Then, the very functional, abstract-everything-we-can approach:
```
function minimise(func, array) {
    var minScore = null;
    var found = null;
    forEach(array, function(element) {
        var score = func(element);
        if (minScore == null || score < minScore) {
            minScore = score;
            found = element;
        }
    });
   return found;
}

function getProperty(propName) {
    return function(object) {
        return object[propName];
    };
}

function shortestRoute(from, to) {
    return minimise(getProperty("length"), possibleRoutes(from, to));
}
```
Unfortunately, it is three times longer than the other version. In programs where you need to minimise several things it might be a good idea to write the generic algorithm like this, so you can re-use it. In most cases the first version is probably good enough.

Note the getProperty function though, it is often useful when doing functional programming with objects.
If we are going to find routes through this map, we will again need a function to create ‘signposts’, lists of directions that can be taken from a given point. Write a function possibleDirections, which takes a point object as argument and returns an array of nearby points. We can only move to adjacent points, both straight and diagonally, so squares have a maximum of eight neighbours. Take care not to return squares that lie outside of the map. For all we know the edge of the map might be the edge of the world.
```
function possibleDirections(from) {
    var mapSize = 20;
    function insideMap(point) {
        return point.x >= 0 && point.x < mapSize &&
               point.y >= 0 && point.y < mapSize;
    }

    var directions = [point(-1, 0), point(1, 0), point(0, -1),
                      point(0, 1), point(-1, -1), point(-1, 1),
                      point(1, 1), point(1, -1)];
    return filter(insideMap, map(partial(addPoints, from), directions));
}

alert(possibleDirections(point(0, 0)));
```
I created a variable mapSize, for the sole purpose of not having to write 20 two times. If, at some other time, we want to use this same function for another map, it would be clumsy if the code was full of 20``s, which all have to be changed. We could even go as far as making the ``mapSize an argument to possibleDirections, so we can use the function for different maps without changing it. I judged that that was not necessary in this case though, such things can always be changed when the need arises.

Then why didn’t I also add a variable to hold the 0, which also occurs two times? I assumed that maps always start at 0, so this one is unlikely to ever change, and using a variable for it only adds noise.
Write a function estimatedDistance that gives an optimistic estimate of the distance between two points. It does not have to look at the height data, but can assume a flat map. Remember that we are only travelling straight and diagonally, and that we are counting the diagonal distance between two squares as 141.
```
function estimatedDistance(pointA, pointB) {
    var dx = Math.abs(pointA.x - pointB.x),
        dy = Math.abs(pointA.y - pointB.y);
    if (dx > dy)
        return (dx - dy) * 100 + dy * 141;
    else
        return (dy - dx) * 100 + dx * 141;
}
```
The strange formulae are used to decompose the path into a straight and a diagonal part. If you have a path like this...

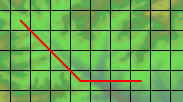
... the path is 8 squares wide and 4 high, so you get 8 - 4 = 4 straight moves, and 4 diagonal ones.

If you wrote a function that just computes the straight “Pythagorean” distance between the points, that would also work. What we need is an optimistic estimate, and assuming you can go straight to the goal is certainly optimistic. However, the closer the estimate is to the real distance, the less useless paths our program has to try out.
We will use a binary heap for the open list. What would be a good data structure for the reached list? This one will be used to look up routes, given a pair of x, y coordinates. Preferably in a way that is fast. Write three functions, makeReachedList, storeReached, and findReached. The first one creates your data structure, the second one, given a reached list, a point, and a route, stores a route in it, and the last one, given a reached list and point, retrieves a route or returns undefined to indicate that no route was found for that point.

One reasonable idea would be to use an object with objects in it. One of the coordinates in the points, say x, is used as a property name for the outer object, and the other, y, for the inner object. This does require some bookkeeping to handle the fact that, sometimes, the inner object we are looking for is not there (yet).
```
function makeReachedList() {
    return {};
}

function storeReached(list, point, route) {
    var inner = list[point.x];
    if (inner == undefined) {
        inner = {};
        list[point.x] = inner;
    }
    inner[point.y] = route;
}

function findReached(list, point) {
    var inner = list[point.x];
    if (inner == undefined)
        return undefined;
    else
        return inner[point.y];
}
```
Another possibility is to merge the x and y of the point into a single property name, and use that to store routes in a single object.
```
function pointID(point) {
    return point.x + "-" + point.y;
}

function makeReachedList() {
    return {};
}

function storeReached(list, point, route) {
    list[pointID(point)] = route;
}

function findReached(list, point) {
    return list[pointID(point)];
}
```

Navigation

Chapter 10 Exercise Set 1¶

Navigation